题目内容
已知圆C: ,直线L:
,直线L:
(1)求证:对m ,直线L与圆C总有两个交点;
,直线L与圆C总有两个交点;
(2)设直线L与圆C交于点A、B,若|AB|= ,求直线L的倾斜角;
,求直线L的倾斜角;
(3)设直线L与圆C交于A、B,若定点P(1,1)满足 ,求此时直线L的方程.
,求此时直线L的方程.
 ,直线L:
,直线L:
(1)求证:对m
 ,直线L与圆C总有两个交点;
,直线L与圆C总有两个交点;(2)设直线L与圆C交于点A、B,若|AB|=
 ,求直线L的倾斜角;
,求直线L的倾斜角;(3)设直线L与圆C交于A、B,若定点P(1,1)满足
 ,求此时直线L的方程.
,求此时直线L的方程.(1)略(2) (3)x-y=0或x+y-2=0
(3)x-y=0或x+y-2=0
 (3)x-y=0或x+y-2=0
(3)x-y=0或x+y-2=0本试题主要是考查了直线与圆的位置关系,以及向量的知识综合运用。
(1)要证明直线与圆总有公共点,则说明圆心到直线的距离小于圆的半径即可。
(2)设出直线方程,利用联立方程组,通过弦长公式得到斜率K的值,进而得到直线方程。
(3)设出点A,B的坐标,然后利用向量关系式得到坐标关系,进而联立方程组结合韦达定理得到结论。
(1)要证明直线与圆总有公共点,则说明圆心到直线的距离小于圆的半径即可。
(2)设出直线方程,利用联立方程组,通过弦长公式得到斜率K的值,进而得到直线方程。
(3)设出点A,B的坐标,然后利用向量关系式得到坐标关系,进而联立方程组结合韦达定理得到结论。

练习册系列答案
相关题目
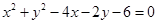 的圆心在直线
的圆心在直线 上,其中
上,其中 ,则
,则 的最小值是 .
的最小值是 . 的一个焦点是圆
的一个焦点是圆 的圆心,且虚轴长为
的圆心,且虚轴长为 ,则双曲线的离心率为
,则双曲线的离心率为 
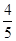

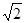
 、
、 分别为不等边
分别为不等边 的重心与外心
的重心与外心 、
、 且
且 平行于
平行于
 点的轨迹
点的轨迹 的方程
的方程
 过点
过点 并与曲线
并与曲线 、
、 两点
两点 且以
且以 为直径的
为直径的 若存在
若存在 所截得的弦长为
所截得的弦长为 ,则实数
,则实数 的值为( )
的值为( )
 的顶点
的顶点 ,重心
,重心
 上任意一点,则
上任意一点,则 的取值范围是
的取值范围是



 相切,
相切, 两点,当
两点,当 时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由. 的度数是50°,∠OBC=40°,则∠OAC等于
的度数是50°,∠OBC=40°,则∠OAC等于