题目内容
(本小题满分12分)已知圆 :
: ,是否存在斜率为
,是否存在斜率为 的直线
的直线 ,使
,使 被圆
被圆 截得的弦
截得的弦 为直径的圆经过原点,若存在,求出直线
为直径的圆经过原点,若存在,求出直线 的方程,若不存在说明理由.
的方程,若不存在说明理由.
 :
: ,是否存在斜率为
,是否存在斜率为 的直线
的直线 ,使
,使 被圆
被圆 截得的弦
截得的弦 为直径的圆经过原点,若存在,求出直线
为直径的圆经过原点,若存在,求出直线 的方程,若不存在说明理由.
的方程,若不存在说明理由.存在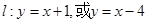 满足要求,理由见解析
满足要求,理由见解析
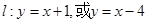 满足要求,理由见解析
满足要求,理由见解析试题分析:假设存在,设
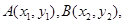 直线
直线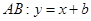 ,
,因为以弦
 为直径的圆经过原点,所以
为直径的圆经过原点,所以 ,所以
,所以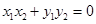 .
.由
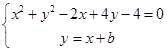 得:
得: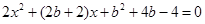 ,
,所以
 ,解得
,解得 或
或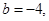
所以存在
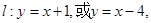 满足要求. ---12分
满足要求. ---12分点评:将以弦
 为直径的圆经过原点,转化为
为直径的圆经过原点,转化为 是解决本小题的关键.
是解决本小题的关键.
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 :
: ,直线
,直线 被圆所截得的弦的中点为P(5,3).(1)求直线
被圆所截得的弦的中点为P(5,3).(1)求直线 :
: 与圆
与圆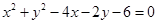 的圆心在直线
的圆心在直线 上,其中
上,其中 ,则
,则 的最小值是 .
的最小值是 .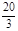 ,椭圆C2的方程为
,椭圆C2的方程为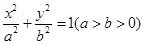 ,C2的离心率为
,C2的离心率为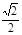 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
 ,圆
,圆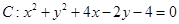 .
. ,直线
,直线 恒过一定点N,且直线
恒过一定点N,且直线
 的交于A、B两点,与圆D:
的交于A、B两点,与圆D: (异于C、N),当
(异于C、N),当 变化时,求证
变化时,求证 的弦MN的中点,则弦MN所在直线的方程为( )
的弦MN的中点,则弦MN所在直线的方程为( )



 的一个焦点是圆
的一个焦点是圆 的圆心,且虚轴长为
的圆心,且虚轴长为 ,则双曲线的离心率为
,则双曲线的离心率为 
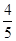

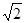
 、
、 分别为不等边
分别为不等边 的重心与外心
的重心与外心 、
、 且
且 平行于
平行于
 点的轨迹
点的轨迹 的方程
的方程
 过点
过点 并与曲线
并与曲线 、
、 两点
两点 且以
且以 为直径的
为直径的 若存在
若存在 相切,
相切, 两点,当
两点,当 时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.