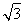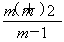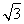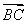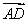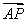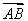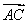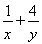题目内容
如图，在矩形ABCD中，AB＝
，BC＝2，点E为BC的中点，点F在边CD上．若
·
＝
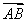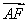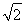，则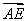
·
＝________．
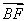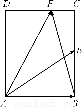
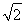
【解析】(解法1)由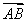
·
＝
，
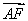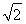得|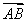|·||·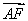cos∠FAB＝
.
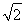由矩形的性质，得|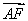|·cos∠FAB＝DF.
∵AB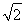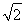＝，∴·DF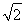＝，∴DF＝1.
∴CF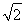＝－1.
记
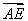和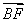
之间的夹角为θ，∠AEB＝α，∠FBC＝β，则θ＝α＋β.
又∵BC＝2，点E为BC的中点，∴BE＝1.
∴
·
＝|
|·|
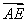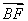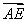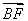|·cosθ
＝|
|·|
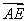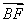|·cos(α＋β)
＝|
|·|
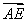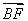|·(cosαcosβ－sinαsinβ)
＝|
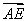|cosα·|
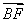|·cosβ－|
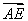|sinα·|
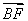|sinβ
＝BE·BC－AB·CF＝1×2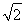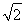－(－1)＝.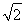
(解法2)以A为坐标原点、AB为x轴建立直角坐标系，则B(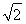
，0)，D(0，2)，C(
，2)，E(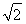
，1)，可设F(x，2)．
由·＝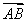
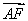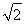，计算可得x＝1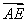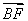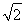，·＝(，1)·(1－
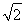，2)＝.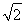
练习册系列答案
相关题目
