题目内容
已知非零向量a、b、c满足a+b+c=0,向量a、b的夹角为120°,且|b|=2|a|,则向量a与c的夹角为________.
90°
【解析】由题意,得c=-a-b,a·c=-a2-a·b=-|a|2-|a||b|cos120°=-|a|2+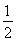 |a||b|=-|a|2+
|a||b|=-|a|2+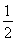 |a|·2|a|=-|a|2+|a|2=0,所以a⊥c,即a与c的夹角为90°
|a|·2|a|=-|a|2+|a|2=0,所以a⊥c,即a与c的夹角为90°

练习册系列答案
相关题目
题目内容
已知非零向量a、b、c满足a+b+c=0,向量a、b的夹角为120°,且|b|=2|a|,则向量a与c的夹角为________.
90°
【解析】由题意,得c=-a-b,a·c=-a2-a·b=-|a|2-|a||b|cos120°=-|a|2+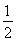 |a||b|=-|a|2+
|a||b|=-|a|2+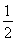 |a|·2|a|=-|a|2+|a|2=0,所以a⊥c,即a与c的夹角为90°
|a|·2|a|=-|a|2+|a|2=0,所以a⊥c,即a与c的夹角为90°
