题目内容
△ABC的外接圆的圆心为O,半径为1,2
+
+
=
且|
|=|
|,则
•
的值等于( )
| OA |
| AB |
| AC |
| 0 |
| OA |
| AB |
| BA |
| BC |
| A、1 | ||
B、
| ||
| C、-1 | ||
D、-
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据已知条件容易得到
=-
,所以OB,OC在一条直线上,即都在边BC上,再根据|
|=|
|可得到∠ABC=60°,|
|=2,所以根据数量积的计算公式即可求得
•
.
| OB |
| OC |
| OA |
| AB |
| BC |
| BA |
| BC |
解答:
解:2
+
+
=
+
+
-
=
;
∴
=-
,且|
|=|
|=1,∴图形如下:
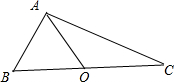 ∴∠ABC=60°;
∴∠ABC=60°;
∴
•
=2cos60°=1.
故选A.
| OA |
| AB |
| AC |
| OA |
| OB |
| OC |
| OA |
| 0 |
∴
| OB |
| OC |
| OA |
| AB |
 ∴∠ABC=60°;
∴∠ABC=60°;∴
| BA |
| BC |
故选A.
点评:考查向量的加法、减法运算,共线向量基本定理,外接圆的概念,以及数量积的计算公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设向量
=(-1,2)
=(2,-1),则(
•
)(
+
)等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(1,1) |
| B、(-4,-4) |
| C、-4 |
| D、(-2,-2) |
若sinα=3cosα,则sin2α-3sinαcosα+1的值是( )
| A、-1 | B、1 | C、0 | D、2 |
函数y=log2(x2-4)的定义域为( )
| A、R |
| B、(-∞,-2)∪(2,+∞) |
| C、(-∞,2)∪(2,+∞) |
| D、(2,+∞) |
设点P是椭圆
+
=1(a>b>0)上异于顶点的任意点,作△PF1F2的左、右旁切圆,与x轴的切点为D,则点D( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、在椭圆内 | B、在椭圆外 |
| C、在椭圆上 | D、以上都有可能 |
下列各角中,为第三象限的角是( )
| A、270° | B、690° |
| C、-129° | D、-230° |
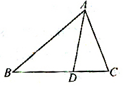 在△ABC中,∠A=60°,且∠A的平分线AD将BC分成两段之比为BD:DC=2:1,又AD=
在△ABC中,∠A=60°,且∠A的平分线AD将BC分成两段之比为BD:DC=2:1,又AD=