题目内容
函数y=log2(x2-4)的定义域为( )
| A、R |
| B、(-∞,-2)∪(2,+∞) |
| C、(-∞,2)∪(2,+∞) |
| D、(2,+∞) |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:要使函数有意义,则需x2-4>0,解得即可得到定义域.
解答:
解:要使函数有意义,则需
x2-4>0,
解得,x>2或x<-2.
则定义域为:(-∞,-2)∪(2,+∞).
故选B.
x2-4>0,
解得,x>2或x<-2.
则定义域为:(-∞,-2)∪(2,+∞).
故选B.
点评:本题考查函数的定义域的求法,注意对数的真数大于0,考查运算能力,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
一物体的运动方程是s=3+t2,则在t=2时刻的瞬时速度为( )
| A、3 | B、4 | C、5 | D、7 |
已知集合M={y|y=2|x|,x∈R},N={x|y=lg(3-x)},且全集I=R,则(∁IM)∩N( )
| A、[3,+∞) | B、[1,3) |
| C、(-∞,1) | D、φ |
△ABC的外接圆的圆心为O,半径为1,2
+
+
=
且|
|=|
|,则
•
的值等于( )
| OA |
| AB |
| AC |
| 0 |
| OA |
| AB |
| BA |
| BC |
| A、1 | ||
B、
| ||
| C、-1 | ||
D、-
|
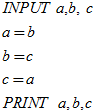 以下程序输入2,3,4运行后,输出的结果是
以下程序输入2,3,4运行后,输出的结果是