题目内容
设点P是椭圆
+
=1(a>b>0)上异于顶点的任意点,作△PF1F2的左、右旁切圆,与x轴的切点为D,则点D( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、在椭圆内 | B、在椭圆外 |
| C、在椭圆上 | D、以上都有可能 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先作出一个旁切圆(如左切圆),设圆与x轴(即线段F2F1的延长线)相切于点C,与线段F2P的延长线相切于点D,与线段PF1相切于点E,根据图形的几何特征,并利用椭圆定义,及圆的切线性质,得CF2=a+c,从而可确定C点的位置,同理可得其它两个旁切圆与x轴相切时切点的位置.
解答:
解:如图1所示,△PF1F2的一个旁切圆与x轴(即线段F2F1的延长线)相切于点C,
与线段F2P的延长线相切于点D,与线段PF1相切于点E.
由椭圆的定义,得|PF1|+|PF2|=2a,
由圆的切线性质,得|F2D|=|F2C|,|PD|=|PE|,|CF1|=|EF1|,
于是|F2C|=|F2D|=|F2P|+|PD|=2a-|F1P|+|PD|=2a-(|F1P|-|PD|)
=2a-(|F1P|-|PE|)=2a-|EF1|=2a-CF1=a+(a+|CF1|)=a+c.
故切点C为椭圆的左顶点.
同理,旁切圆与x轴相切时切点的位置为椭圆的右顶点,如图2所示.
故选C.

与线段F2P的延长线相切于点D,与线段PF1相切于点E.
由椭圆的定义,得|PF1|+|PF2|=2a,
由圆的切线性质,得|F2D|=|F2C|,|PD|=|PE|,|CF1|=|EF1|,
于是|F2C|=|F2D|=|F2P|+|PD|=2a-|F1P|+|PD|=2a-(|F1P|-|PD|)
=2a-(|F1P|-|PE|)=2a-|EF1|=2a-CF1=a+(a+|CF1|)=a+c.
故切点C为椭圆的左顶点.
同理,旁切圆与x轴相切时切点的位置为椭圆的右顶点,如图2所示.
故选C.
点评:本题考查了椭圆的定义及圆的切线的性质,关键是将各线段的长度进行转化.求解时应注意以下常见结论:
(1)若P为椭圆上任意一点,F1,F2是椭圆的两个焦点,则|PF1|+|PF2|=2a;
(2)从圆外一点M向圆引切线,设切点分别为A,B,则|MA|=|MB|;
(3)椭圆焦点到对应顶点的距离等于a-c,焦点到另一焦点对应顶点的距离等于a+c.
(1)若P为椭圆上任意一点,F1,F2是椭圆的两个焦点,则|PF1|+|PF2|=2a;
(2)从圆外一点M向圆引切线,设切点分别为A,B,则|MA|=|MB|;
(3)椭圆焦点到对应顶点的距离等于a-c,焦点到另一焦点对应顶点的距离等于a+c.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC的外接圆的圆心为O,半径为1,2
+
+
=
且|
|=|
|,则
•
的值等于( )
| OA |
| AB |
| AC |
| 0 |
| OA |
| AB |
| BA |
| BC |
| A、1 | ||
B、
| ||
| C、-1 | ||
D、-
|
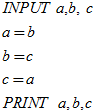 以下程序输入2,3,4运行后,输出的结果是
以下程序输入2,3,4运行后,输出的结果是