题目内容
(本小题满分14分)椭圆E中心在原点O,焦点在x轴上,其离心率e=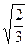 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段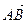 的比为2.
的比为2.
(1)用直线l的斜率k(k≠0)表示△OAB的面积;
(2)当△OAB的面积最大时,求椭圆E的方程.
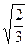 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段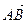 的比为2.
的比为2.(1)用直线l的斜率k(k≠0)表示△OAB的面积;
(2)当△OAB的面积最大时,求椭圆E的方程.
(1)S△OAB= (k≠0).;(2)x2+3y2=5.
(k≠0).;(2)x2+3y2=5.
 (k≠0).;(2)x2+3y2=5.
(k≠0).;(2)x2+3y2=5. 解:(1)设椭圆E的方程为 =1(a>b>0),由e=
=1(a>b>0),由e= .
.
∴a2=3b2,故椭圆方程x2+3y2=3b2. 2分
设A(x1,y1)、B(x2,y2),由于点C(-1,0)分有向线段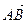 的比为2,
的比为2,
∴ ,即
,即 由
由 消去y整理并化简,得(3k2+1)x2+6k2x+3k2-3b2=0. 4分
消去y整理并化简,得(3k2+1)x2+6k2x+3k2-3b2=0. 4分
由直线l与椭圆E相交于A(x1,y1)、B(x2,y2)?两点,?
∴ 而S△OAB=
而S△OAB= |y1-y2|=
|y1-y2|= |-2y2-y2|
|-2y2-y2|
= |y2|=
|y2|= |k(x2+1)|=
|k(x2+1)|=  |k||x2+1|. ⑥
|k||x2+1|. ⑥
由①④得:x2+1=-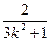 ,代入⑥得:
,代入⑥得:
S△OAB= (k≠0). 8分
(k≠0). 8分
(2)因S△OAB= =
= ≤
≤ =
=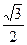 ,
,
当且仅当k=± ,S△OAB取得最大值.
,S△OAB取得最大值.
此时x1+x2=-1,又∵ =-1,
=-1,
∴x1=1,x2=-2.
将x1,x2及k2= 代入⑤得3b2=5.
代入⑤得3b2=5.
∴椭圆方程x2+3y2=5. 14分
 =1(a>b>0),由e=
=1(a>b>0),由e= .
.∴a2=3b2,故椭圆方程x2+3y2=3b2. 2分
设A(x1,y1)、B(x2,y2),由于点C(-1,0)分有向线段
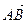 的比为2,
的比为2,
|
 ,即
,即 由
由 消去y整理并化简,得(3k2+1)x2+6k2x+3k2-3b2=0. 4分
消去y整理并化简,得(3k2+1)x2+6k2x+3k2-3b2=0. 4分由直线l与椭圆E相交于A(x1,y1)、B(x2,y2)?两点,?
|
 而S△OAB=
而S△OAB= |y1-y2|=
|y1-y2|= |-2y2-y2|
|-2y2-y2|=
 |y2|=
|y2|= |k(x2+1)|=
|k(x2+1)|=  |k||x2+1|. ⑥
|k||x2+1|. ⑥由①④得:x2+1=-
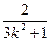 ,代入⑥得:
,代入⑥得:S△OAB=
 (k≠0). 8分
(k≠0). 8分(2)因S△OAB=
 =
= ≤
≤ =
=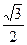 ,
,当且仅当k=±
 ,S△OAB取得最大值.
,S△OAB取得最大值.此时x1+x2=-1,又∵
 =-1,
=-1,∴x1=1,x2=-2.
将x1,x2及k2=
 代入⑤得3b2=5.
代入⑤得3b2=5.∴椭圆方程x2+3y2=5. 14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 时,求直线l的方程;
时,求直线l的方程; 为定值.
为定值. 的最小值.
的最小值.
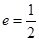 ,求
,求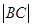 与
与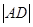 的比值;
的比值; 的焦点,斜率为
的焦点,斜率为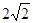 的直线交抛物线于
的直线交抛物线于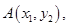
 (
( )两点,且
)两点,且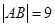 .
.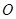 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若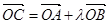 ,求
,求 的值.
的值.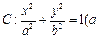 >
> >0
>0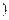 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为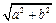 的圆是椭圆
的圆是椭圆 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为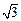 .
. 的直线
的直线 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆 是椭圆
是椭圆 ,使得
,使得 与椭圆
与椭圆 ⊥
⊥ .
.



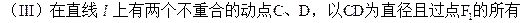

 是椭圆
是椭圆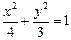 上一动点,点
上一动点,点 是点
是点 在
在 轴上的射影,坐标平面
轴上的射影,坐标平面 内动点
内动点 (
( 为坐标原点),设动点
为坐标原点),设动点 .
.
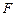 的直线
的直线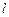 交曲线
交曲线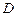 ,
,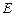 两点,且
两点,且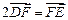 ,点
,点 ,求直线
,求直线 的方程.
的方程.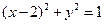 都相切,则双曲线C的离心率是____;
都相切,则双曲线C的离心率是____;