题目内容
6.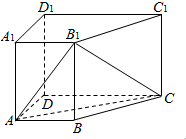 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).(1)求证:平面CDB1⊥平面ADD1A1;
(2)若直线AA1与平面AB1C所成角的正弦值为$\frac{6}{7}$,求四面体B-AB1C的体积.
分析 (1)取CD的中点E,连结BE,证明BE⊥CD,可得CD⊥AD,利用AA1⊥平面ABCD,可得AA1⊥CD,证明CD⊥平面ADD1A1,即可证明平面CDB1⊥平面ADD1A1;
(2)以D为原点,$\overrightarrow{DA}$,$\overrightarrow{DC}$,$\overrightarrow{D{D}_{1}}$的方向为x,y,z轴的正方向建立空间直角坐标系,求出平面AB1C的法向量,利用直线AA1与平面AB1C所成角的正弦值为$\frac{6}{7}$,建立方程,可求k的值,即可求四面体B-AB1C的体积.
解答 (1)证明:取CD的中点E,连结BE.
∵AB∥DE,AB=DE=3k,∴四边形ABED为平行四边形,…(2分)
∴BE∥AD且BE=AD=4k.
在△BCE中,∵BE=4k,CE=3k,BC=5k,∴BE2+CE2=BC2,
∴∠BEC=90°,即BE⊥CD,
又∵BE∥AD,∴CD⊥AD. …(4分)
∵AA1⊥平面ABCD,CD?平面ABCD,
∴AA1⊥CD.又AA1∩AD=A,
∴CD⊥平面ADD1A1.
∵CD?平面CDB1,
∴平面CDB1⊥平面ADD1A1;…(6分)
(2)解:以D为原点,$\overrightarrow{DA}$,$\overrightarrow{DC}$,$\overrightarrow{D{D}_{1}}$的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系,则A(4k,0,0),C(0,6k,0),B1(4k,3k,1),A1(4k,0,1),
∴$\overrightarrow{AC}$=(-4k,6k,0),$\overrightarrow{A{B}_{1}}$=(0,3k,1),$\overrightarrow{A{A}_{1}}$=(0,0,1).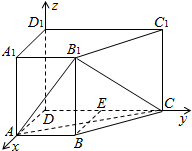
设平面AB1C的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{-4kx+6ky=0}\\{3ky+z=0}\end{array}\right.$
取y=2,得$\overrightarrow{n}$=(3,2,-6k)(k>0). …(9分)
设AA1与平面AB1C所成角为θ,则
sinθ=|cos<$\overrightarrow{A{A}_{1}}$,$\overrightarrow{n}$>|=$\frac{6k}{\sqrt{36{k}^{2}+13}}$=$\frac{6}{7}$,
解得k=1,故所求k的值为1.
∴四面体B-AB1C的体积V=$\frac{1}{3}•\frac{1}{2}•AB•AD•B{B}_{1}$=$\frac{1}{3}•\frac{1}{2}•3•4•1$=2…(12分)
点评 本题考查棱柱的结构特征,考查线面垂直面面垂直,考查四面体B-AB1C的体积,考查空间想象能力,逻辑思维能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (1,+∞) | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | [$\frac{\sqrt{6}}{2}$,+∞) | D. | (1,2] |
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
 如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.