抛物线$y=\frac{1}{8}{x^2}$的焦点到双曲线${y^2}-\frac{x^2}{3}=1$的一条渐近线的距离为( )A．1B．2C．$\sqrt{3}$D．$2\sqrt{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．抛物线$y=\frac{1}{8}{x^2}$的焦点到双曲线${y^2}-\frac{x^2}{3}=1$的一条渐近线的距离为（　　）

A．

B．

C．

$\sqrt{3}$

D．

$2\sqrt{3}$

分析求出抛物线的焦点和双曲线的渐近线方程，再由点到直线的距离公式计算即可得到所求．

解答解：抛物线$y=\frac{1}{8}{x^2}$的焦点为（0，2），
双曲线${y^2}-\frac{x^2}{3}=1$的一条渐近线为y=$\frac{\sqrt{3}}{3}$x，
则焦点到渐近线的距离为d=$\frac{2}{\sqrt{\frac{1}{3}+1}}$$\sqrt{3}$．
故选：C．

点评本题考查抛物线和双曲线的性质，主要考查渐近线方程和焦点坐标，运用点到直线的距离公式是解题的关键．

练习册系列答案

相关题目

4．

如图，已知AB为半圆O的直径，AB=4，C为平面上一点，过点C作半圆的切线CD，过A点作AD⊥CD于D，角半圆于点E，DE=1，则BC的长为（　　）

5．已知A（1，5），B（5，-2），在x轴上存在一点M，使|MA|=|MB|，则点M的坐标为（　　）

2．已知函数f（x）=$\sqrt{3}$sinπx-sin（πx+$\frac{π}{6}$），x∈R．
（1）求y=f（x）的正零点；
（2）设f（x）的所有正零点依次组成数列{a_n}，数列{b_n}满足b₁=0，b_n+1-b_n=a_n，n∈N^*，求{b_n}的通项公式．

9．直线x-2y+2=0经过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$（a＞0，b＞0）的两个顶点．
（1）求椭圆C的方程；
（2）已知抛物线D：y=x²+$\frac{1}{4}$，点M在抛物线D上运动，直线l：y=x+m（m∈[-$\sqrt{2}$，-1]）交椭圆C于点N，P，求△MNP面积的最小值．

19．若两直线l₁：ax+2y+a-2=0与l₂：（a-2）x+4y+2=0互相平行，则常数a=-2．

6．

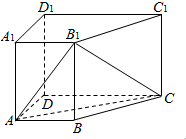如图，在四棱柱ABCD-A₁B₁C₁D₁中，侧棱AA₁⊥底面ABCD，AB∥DC，AA₁=1，AB=3k，AD=4k，BC=5k，DC=6k（k＞0）．
（1）求证：平面CDB₁⊥平面ADD₁A₁；
（2）若直线AA₁与平面AB₁C所成角的正弦值为$\frac{6}{7}$，求四面体B-AB₁C的体积．

3．对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[-1.08]=-2，定义函数f（x）=x-[x]，给定下列叙述：①函数f（x）的最大值为1；②函数f（x）的最小值为0；③函数G（x）=f（x）-$\frac{1}{2}$有无数个零点；④函数f（x）是增函数．其中正确的个数为（　　）

4．

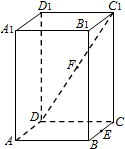在正四棱柱ABCD-A₁B₁C₁D₁中，E是BC的中点，F是C₁D的中点，P是棱CC₁所在直线上的动点．则下列四个命题：
①CD⊥PE
②EF∥平面ABC₁
③${V_{P-{A_1}D{D_1}}}={V_{{D_1}-ADE}}$
④不存在过P的直线与正四棱柱的各个面都成等角．
其中正确命题的序号是①③（写出所有正确命题的序号）．

试题分类