题目内容
16.已知F1,F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,P为以双曲线的焦距2c为直径的圆与双曲线的一个交点,若△PF1F2面积的最小值为$\frac{1}{2}$a2,则双曲线的离心率e的取值范围是( )| A. | (1,+∞) | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | [$\frac{\sqrt{6}}{2}$,+∞) | D. | (1,2] |
分析 由题意得,△PF1F2为以P为直角顶点的直角三角形,$\frac{1}{2}$|PF1|•|PF2|≥$\frac{1}{2}$a2,即|PF1|•|PF2|≥a2,再由勾股定理和双曲线的定义,结合离心率公式,计算即可得到所求范围.
解答 解:由题意得,△PF1F2为以P为直角顶点的直角三角形,
$\frac{1}{2}$|PF1|•|PF2|≥$\frac{1}{2}$a2,即|PF1|•|PF2|≥a2,
则4c2=${\left|P{F}_{2}\right|}^{2}$+${\left|P{F}_{1}\right|}^{2}={(\right|P{F}_{1}|-|P{F}_{2}\left|)}^{2}$+2|PF1||PF2|
≥4a2+2a2=6a2,
则e=$\frac{c}{a}$≥$\frac{\sqrt{6}}{2}$,
故选:C.
点评 本题突出考查双曲线的定义、方程、性质,注重通性通法.另外试题构造了最小值情境,背景新颖,为考生灵活运用数学知识、思想方法解决实际问题提供了广阔的空间.

练习册系列答案
相关题目
8.已知复数 $z=\frac{1-i}{i}$的共轭复数为( )
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
5.已知A(1,5),B(5,-2),在x轴上存在一点M,使|MA|=|MB|,则点M的坐标为( )
| A. | $(\frac{8}{3},0)$ | B. | $(\frac{3}{8},0)$ | C. | $(-\frac{8}{3},0)$ | D. | $(-\frac{3}{8},0)$ |
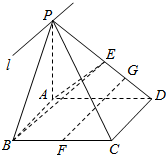 如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.
如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l. 如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )
如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( ) 如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.
如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.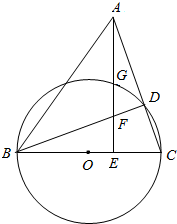 如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.
如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.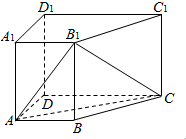 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).