题目内容
16.已知函数$f(x)=\left\{{\;}\right._{2f(x-2),x∈(0,+∞)}^{1-|x+1|,x∈[-2,0]}$,则下列说法中错误的是( )| A. | f(x)的单调递减区间为[2n-3,2n-2](n∈N*) | |
| B. | f(x)的值域为[0,+∞) | |
| C. | 方程f(x)=1在区间[-2,2n]上所有根的个数为2n+1(n∈N) | |
| D. | 若方程f(x)=x+2在区间[-2,4]内有3个不等实根,则实数的取值范围是-2<a≤0 |
分析 作出函数y=f(x)和y=x+a的图象.利用函数y=f(x)的图象及两个图象的交点个数问题确定a的取值范围.
解答 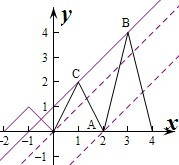 解:若0≤x≤2,则-2≤x-2≤0,
解:若0≤x≤2,则-2≤x-2≤0,
∴f(x)=2f(x-2)=2(1-|x-2+1|)=2-2|x-1|,0≤x≤2.
若2≤x≤4,则0≤x-2≤2,∴f(x)=4-4|x-3|,
如图所示,
由图象可知,f(x)的单调递减区间为[2n-3,2n-2],故A正确;
f(x)的值域为[0,+∞),故B正确;
函数f(x)在[0,+∞)上的对称轴为x=n,∴方程f(x)=1在区间[-2,2n]上所有根的个数为2n+1(n∈N),故C正确;
设y=f(x)和y=x+a,则方程f(x)=x+a在区间[-2,4]内有3个不等实根,、
等价为函数y=f(x)和y=x+a在区间[-2,4]内有3个不同的零点.
作出函数f(x)和y=x+a的图象,如图:
当直线经过点A(2,0)时,两个图象有2个交点,此时直线y=x+a为y=x-2,
当直线经过点O(0,0)时,两个图象有4个交点,此时直线y=x+a为y=x,
当直线经过点B(3,4)和C(1,2)时,两个图象有3个交点,此时直线y=x+a为y=x+1,
∴要使方程f(x)=x+a在区间[-2,4]内有3个不等实根,
则a=1或-2<a<0,故D不正确.
故选:D.
点评 本题主要考查方程根的个数的应用,将方程转化为函数,利用数形结合是解决此类问题的基本方法.

练习册系列答案
相关题目
6.i是虚数单位,若集合S={-1,0,1},则( )
| A. | i3∈S | B. | i6∈S | C. | (-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)3⊆S | D. | {(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)2}⊆S |
 阅读如图所示伪代码,若执行该算法输出的结果是8,则输入的x=4.
阅读如图所示伪代码,若执行该算法输出的结果是8,则输入的x=4.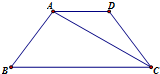 如图,等腰梯形ABCD中,AB=AD=DC=$\frac{1}{2}$BC=1,现将三角形ACD沿AC向上折起,满足平面ABC⊥平面ACD,则三棱锥D-ABC的外接球的表面积为5π.
如图,等腰梯形ABCD中,AB=AD=DC=$\frac{1}{2}$BC=1,现将三角形ACD沿AC向上折起,满足平面ABC⊥平面ACD,则三棱锥D-ABC的外接球的表面积为5π.