题目内容

19．an+1=$\frac{4{a}_{n}-2}{{a}_{n}+7}$，a1=2，求an．

分析 由已知的数列递推式结合不动点法可得数列数列{$\frac{1}{{a}_{n}+1}$}是以$\frac{1}{3}$为首项，以$\frac{1}{5}$为公差的等差数列，求出等差数列的通项公式后可得{an}通项公式．

解答 解：由an+1=$\frac{4{a}_{n}-2}{{a}_{n}+7}$，a1=2，得an+1+1=$\frac{4{a}_{n}-2}{{a}_{n}+7}$+1=$\frac{5{a}_{n}+5}{{a}_{n}+7}$，
∴$\frac{1}{{a}_{n+1}+1}$=$\frac{1}{{a}_{n}+1}$+$\frac{1}{5}$，即$\frac{1}{{a}_{n+1}+1}$-$\frac{1}{{a}_{n}+1}$=$\frac{1}{5}$．
则数列{$\frac{1}{{a}_{n}+1}$}是以$\frac{1}{3}$为首项，以$\frac{1}{5}$为公差的等差数列，
∴$\frac{1}{{a}_{n}+1}$=$\frac{1}{3}$+$\frac{1}{5}（n-1）$=$\frac{3n+2}{15}$，
则an=$\frac{15}{3n+2}$-1．

点评 本题考查了数列递推式，考查了等差关系的确定，考查了等差数列的通项公式，是中档题．

练习册系列答案
相关题目
17．已知函数f（x）=sinx+$\sqrt{3}$cosx
（Ⅰ）求f（x）的周期和振幅；
（Ⅱ）在给出的方格纸上用五点作图法作出f（x）在一个周期内的图象
（Ⅲ）写出函数f（x）的单调递减区间．
10．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左焦点F1坐标为$（{-2\sqrt{2}，0}）$，且椭圆C的短轴长为4，斜率为1的直线l与椭圆G交于A，B两点，以AB为底边的等腰三角形，顶点为P（-3，2）
（1）求椭圆C的方程
（2）求△PAB的面积．
7．甲参加一组投掷保龄球比赛，掷3次，已知甲击中10球的概率是$\frac{1}{4}$，击中9球的概率是$\frac{1}{4}$，击中8球的概率是$\frac{1}{2}$，击中球的个数等于所得到的分数．
（Ⅰ）求甲得到27分的概率；
（Ⅱ）若甲得到的分数是ξ，求ξ的分布列及数学期望．
14．若函数f（x）=ax2+bx+c的值域为[0，+∞），且f（-x）=f（x），x∈R，存在两条都经过点P（1，-2）且互相垂直的直线l1，l2与函数f（x）的图象都没有公共点，则实数a的取值范围是（$\frac{1}{8}$，+∞）．
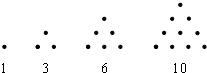4．传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数．他们研究过如图的三角形数：
将三角形数1，3，6，10，…记为数列{an}，将可被5整除的三角形数按从小到大的顺序组成一个新数列
{bn}，可以推测：
（Ⅰ）b2014是数列{an}中的第5035项；
（Ⅱ） b2n-1=$\frac{1}{2}$5n（5n-1）．（用n表示）
11．已知等差数列{an}中，a1+a3+a8=$\frac{5π}{4}$，那么cos（a3+a5）=-$\frac{\sqrt{3}}{2}$．
8．已知角θ的终边经过点P（4，m），且sinθ=$\frac{3}{5}$，则m等于（　　）
A．-3B．3C．$\frac{16}{3}$D．±3
9．如果y=f（x）的定义域为R，对于定义域内的任意x，存在实数a使得f（x+a）=f（-x）成立，则称此函数具有“P（a）性质”．给出下列命题：
①函数y=sinx具有“P（a）性质”；
②若奇函数y=f（x）具有“P（2）性质”，且f（1）=1，则f（2015）=1；
③若函数y=f（x）具有“P（4）性质”，图象关于点（1，0）成中心对称，且在（-1，0）上单调递减，则y=f（x）在（-2，-1）上单调递减，在（1，2）上单调递增；
④若不恒为零的函数y=f（x）同时具有“P（0）性质”和“P（3）性质”，且函数y=g（x）对$?{x_1}，{x_2}∈[{-\frac{1}{2}，\frac{5}{2}}]$，都有|f（x1）-f（x2）|≥2成立，则?x1，x2∈R，都有|f（x1）-f（x2）|≥2成立．其中正确的是①③④（写出所有正确命题的编号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网