题目内容
设a>0，函数f(x)＝x＋
，g(x)＝x－ln x，若对任意的x1，x2∈[1，e]，都有f(x1)≥g(x2)成立，则实数a的取值范围为________．
，g(x)＝x－ln x，若对任意的x1，x2∈[1，e]，都有f(x1)≥g(x2)成立，则实数a的取值范围为________．[
，＋∞)
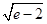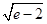，＋∞)问题可转化为f(x)min≥g(x)max，当x∈[1，e]时，g′(x)＝1－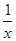
≥0，故g(x)单调递增，则g(x)max＝g(e)＝e－1.又f′(x)＝1－
＝
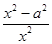，令f′(x)＝0，得x＝a，易知，x＝a是函数f(x)的极小值，当0<a≤1时，f(x)min＝f(1)＝1＋a2，则1＋a2≥e－1，所以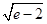≤a≤1；当1<a≤e时，f(x)min＝f(a)＝2a，则2a≥e－1，显然成立，所以1<a≤e；当a>e时，f(x)min＝f(e)＝e＋
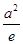，则e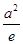＋≥e－1，显然成立，所以a>e.综上，a≥.
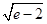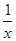≥0，故g(x)单调递增，则g(x)max＝g(e)＝e－1.又f′(x)＝1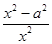－＝，令f′(x)＝0，得x＝a，易知，x＝a是函数f(x)的极小值，当0<a≤1时，f(x)min＝f(1)＝1＋a2，则1＋a2≥e－1，所以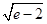≤a≤1；当1<a≤e时，f(x)min＝f(a)＝2a，则2a≥e－1，显然成立，所以1<a≤e；当a>e时，f(x)min＝f(e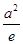)＝e＋，则e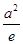＋≥e－1，显然成立，所以a>e.综上，a≥.
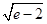练习册系列答案
53随堂测系列答案
相关题目
，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x，y），且0≤θ≤π．
，求f（θ）的值；
上的一个动点，试确定角θ的取值范围，并求函数f（θ）的最小值和最大值．
（分贝）由公式
(
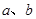为非零常数)给出，其中
为声音能量.
满足
时，求对应的声音能量
满足的等量关系式；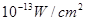
时，声音强度为30分贝；当人们正常说话，声音能量为
时，声音强度为40分贝.当声音能量大于60分贝时属于噪音，一般人在100分贝~120分贝的空间内，一分钟就会暂时性失聪.问声音能量在什么范围时，人会暂时性失聪.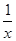
＋2的图象关于点A(0,1)对称．
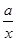，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．
)，B＝[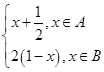
，若x0∈A，且f[f(x0)]∈A，则x0的取值范围是( )
]
]
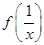＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：
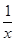；②y＝x＋
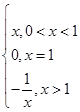，其中满足“倒负”变换的函数是________(填序号)．
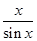，x∈(－π，0)∪(0，π)的图象可能是下列图象中的( )
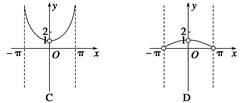
则f(2 016)＝( )
