题目内容
已知函数f(x)的图象与函数h(x)=x+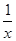 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+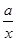 ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
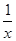 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+
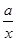 ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.(1)f(x)=x+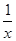
(2)[7,+∞)
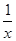
(2)[7,+∞)
解:(1)设f(x)图象上任一点坐标为(x,y),∵点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)的图象上,
∴2-y=-x+ +2,∴y=x+
+2,∴y=x+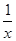 ,即f(x)=x+
,即f(x)=x+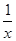 .
.
(2)由题意g(x)=x+ ,且g(x)=x+
,且g(x)=x+ ≥6,x∈(0,2].
≥6,x∈(0,2].
∵x∈(0,2],∴a+1≥x(6-x),
即a≥-x2+6x-1.令q(x)=-x2+6x-1,x∈(0,2],
q(x)=-x2+6x-1=-(x-3)2+8,∴x∈(0,2]时,
q(x)max=q(2)=7,
故a的取值范围为[7,+∞).
∴2-y=-x+
 +2,∴y=x+
+2,∴y=x+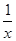 ,即f(x)=x+
,即f(x)=x+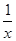 .
.(2)由题意g(x)=x+
 ,且g(x)=x+
,且g(x)=x+ ≥6,x∈(0,2].
≥6,x∈(0,2].∵x∈(0,2],∴a+1≥x(6-x),
即a≥-x2+6x-1.令q(x)=-x2+6x-1,x∈(0,2],
q(x)=-x2+6x-1=-(x-3)2+8,∴x∈(0,2]时,
q(x)max=q(2)=7,
故a的取值范围为[7,+∞).

练习册系列答案
相关题目
 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且 ,则有
,则有 成立,则称
成立,则称 的值;
的值;  在区间
在区间 ,使得
,使得 且
且 , 求证:
, 求证: .
. .
.
 表示
表示 的面积;
的面积; (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为 (
( ).
). 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内? R)万件,要使附加税不少于128万元,则R的取值范围是( )
R)万件,要使附加税不少于128万元,则R的取值范围是( )
 ,g(x)=x-ln x,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为________.
,g(x)=x-ln x,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为________. log2x,则f(2)=________.
log2x,则f(2)=________. 是定义在
是定义在 上的函数,且对任意实数
上的函数,且对任意实数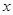 ,都有
,都有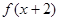 ≤
≤ ,
,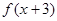 ≥
≥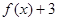 ,且
,且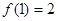 ,
,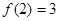 ,则
,则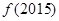 的值是
的值是