题目内容
设集合A=[0, ),B=[
),B=[ ,1],函数f(x)=
,1],函数f(x)=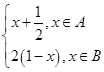 ,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )
,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )
 ),B=[
),B=[ ,1],函数f(x)=
,1],函数f(x)=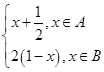 ,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )
,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )A.(0, ] ] | B.( , , ) ) |
C.( , , ] ] | D.[0, ] ] |
B
∵x0∈A,∴f(x0)=x0+ ∈B.
∈B.
∴f[f(x0)]=f(x0+ )=2(1-x0-
)=2(1-x0- )=1-2x0.
)=1-2x0.
又f[f(x0)]∈A,∴0≤1-2x0< ,
,
解得 <x0≤
<x0≤ ,又0≤x0<
,又0≤x0< .
.
∴ <x0<
<x0< ,故选B.
,故选B.
 ∈B.
∈B.∴f[f(x0)]=f(x0+
 )=2(1-x0-
)=2(1-x0- )=1-2x0.
)=1-2x0.又f[f(x0)]∈A,∴0≤1-2x0<
 ,
,解得
 <x0≤
<x0≤ ,又0≤x0<
,又0≤x0< .
.∴
 <x0<
<x0< ,故选B.
,故选B.
练习册系列答案
相关题目
 的函数满足
的函数满足 ,且
,且 ,若
,若 ,则
,则 ( )
( )




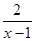 的定义域是(-∞,1)∪[2,5),则其值域是( )
的定义域是(-∞,1)∪[2,5),则其值域是( ) ,2]
,2] ,g(x)=x-ln x,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为________.
,g(x)=x-ln x,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为________.
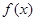 是定义在
是定义在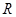 上的函数,且对任意实数
上的函数,且对任意实数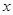 ,都有
,都有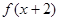 ≤
≤ ,
,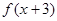 ≥
≥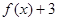 ,且
,且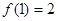 ,
,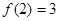 ,则
,则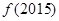 的值是
的值是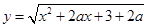 的值域为
的值域为 ,则
,则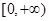 的取值范围是________
的取值范围是________