题目内容
已知函数y=f(x)是定义在R上的奇函数,且当x<0时,不等式f(x)+xf′(x)<0成立,若a=30.3f(30.3),b=logπ3f(logπ3),c=log3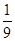 f
f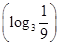 ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ).
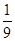 f
f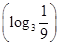 ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ).| A.a>b>c | B.c>b>a |
| C.c>a>b | D.a>c>b |
C
设g(x)=xf(x),则g′(x)=f(x)+xf′(x)<0(x<0),∴当x<0时,g(x)=xf(x)为减函数.
又g(x)为偶函数,∴当x>0时,g(x)为增函数.
∵1<30.3<2,0<logπ3<1,log3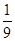 =-2,
=-2,
∴g(-2)>g(30.3)>g(logπ3),即c>a>b.
又g(x)为偶函数,∴当x>0时,g(x)为增函数.
∵1<30.3<2,0<logπ3<1,log3
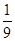 =-2,
=-2,∴g(-2)>g(30.3)>g(logπ3),即c>a>b.

练习册系列答案
相关题目
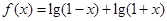 ,
,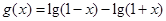 ,则( )
,则( )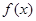 与
与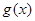 均为偶函数
均为偶函数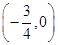 成中心对称,对任意实数x都有f(x)=-
成中心对称,对任意实数x都有f(x)=- ,且f(-1)=1,f(0)=-2,则f(0)+f(1)+…+f(2013)=________.
,且f(-1)=1,f(0)=-2,则f(0)+f(1)+…+f(2013)=________.
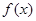 是定义在
是定义在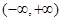 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数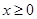 ,都有
,都有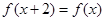 ,且当
,且当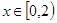 时,
时,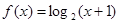 ,则
,则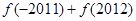 的值为( )
的值为( )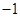
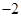
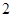
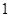
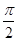 的奇函数
的奇函数