题目内容
已知函数f(x)=ax3+bsin x+4(a,b∈R),f(lg(log210))=5,则f(lg(lg 2))等于 ( ).
| A.-5 | B.-1 |
| C.3 | D.4 |
C
令g(x)=f(x)-4=ax3+bsin x是奇函数,又lg(log210)=lg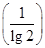 =-lg(lg 2).
=-lg(lg 2).
∴g[lg(log210)]=g[-lg(lg 2)]=-g[lg(lg 2)].
∴f[lg(log210)]-4=-(f[lg(lg 2)]-4).
因此f[lg(lg 2)]=4-1=3.
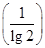 =-lg(lg 2).
=-lg(lg 2).∴g[lg(log210)]=g[-lg(lg 2)]=-g[lg(lg 2)].
∴f[lg(log210)]-4=-(f[lg(lg 2)]-4).
因此f[lg(lg 2)]=4-1=3.

练习册系列答案
相关题目
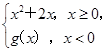 为奇函数,则f(g(-1))=( )
为奇函数,则f(g(-1))=( )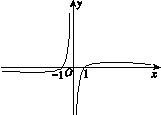
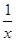
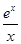
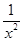 -1
-1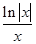
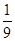 f
f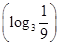 ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ).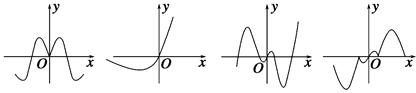
 上的偶函数
上的偶函数 ,当
,当 x≥0时,
x≥0时, ,则满足
,则满足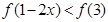 的x取值范围是( )
的x取值范围是( )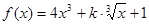 (
(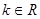 ),若
),若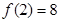 ,则
,则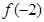 的值为___________.
的值为___________.