题目内容
命题“存在 ,使
,使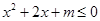 ”的否定是( )
”的否定是( )
A.存在 ,使 ,使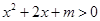 |
B.不存在 ,使 ,使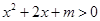 |
C.对于任意 ,都有 ,都有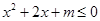 |
D.对于任意 ,都有 ,都有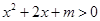 |
D
解析试题分析:特称命题的否定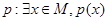 ;它的否定
;它的否定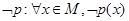 ,∴命题“存在
,∴命题“存在 ,使
,使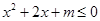 ”的否定是“对于任意
”的否定是“对于任意 ,都有
,都有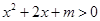 ”
”
考点:特称命题的否定.

练习册系列答案
相关题目
给定两个命题p,q.若﹁p是q的必要而不充分条件,则p是﹁q的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设原命题:若a+b≥2,则a,b中至少有一个不小于1.则原命题与其逆命题的真假情况是( )
| A.原命题真,逆命题假 | B.原命题假,逆命题真 |
| C.原命题与逆命题均为真命题 | D.原命题与逆命题均为假命题 |
设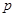 ∶
∶ ∶
∶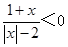 ,则
,则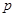 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出定义:若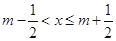 (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数 最近的整数,记作
最近的整数,记作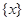 ,即
,即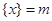 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数 的四个命题:
的四个命题:
①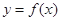 的定义域是
的定义域是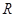 ,值域是
,值域是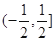 ;②点
;②点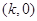 是
是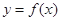 的图像的对称中心,其中
的图像的对称中心,其中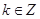 ;③函数
;③函数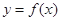 的最小正周期为1;④函数
的最小正周期为1;④函数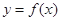 在
在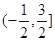 上是增函数.则上述命题中真命题的序号是( )
上是增函数.则上述命题中真命题的序号是( )
| A.①④ | B.①③ | C.②③ | D.②④ |
下列有关命题说法正确的是( )
A.命题p:“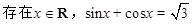 ”,则Øp是假命题 ”,则Øp是假命题 |
B. ”的充分必要条件 ”的充分必要条件 |
C.命题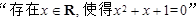 的否定是:“ 的否定是:“ ” ” |
D.命题“若tanα≠1,则α≠ ” 的逆否命题是真命题 ” 的逆否命题是真命题 |
下列说法中,正确的是( )
A.命题“若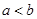 ,则 ,则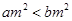 ”的否命题是假命题. ”的否命题是假命题. |
B.设 为两个不同的平面,直线 为两个不同的平面,直线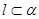 ,则“ ,则“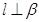 ”是 “ ”是 “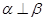 ” 成立的充分不必要条件. ” 成立的充分不必要条件. |
C.命题“存在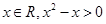 ”的否定是“对任意 ”的否定是“对任意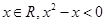 ”. ”. |
D.已知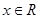 ,则“ ,则“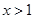 ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
实数 ,条件
,条件 :
: ,条件
,条件 :
: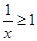 ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若数列{ }通项为
}通项为 =an,则“数列{
=an,则“数列{ }为递增数列”的一个充分不必要条件是( )
}为递增数列”的一个充分不必要条件是( )
| A.a≥0 | B.a>1 | C.a>0 | D.a<0 |