题目内容
【题目】设直线l的方程为(a﹣1)x+y+a+3=0,(a∈R).
(1)若直线l在两坐标轴上截距的绝对值相等,求直线l的方程;
(2)若直线l不经过第一象限,求实数a的取值范围.
【答案】(1)﹣4x+y=0,﹣x+y+3=0或x+y+5=0.(2)a≥﹣1.
【解析】
(1)由直线截距的概念,列方程![]() 求解即可;
求解即可;
(2)先讨论直线的斜率是否存在,然后分情况讨论截距是否为0,再列不等式组运算即可得解.
解:(1)由直线l在两坐标轴上截距的绝对值相等,可得![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]()
![]() ,
,
由已知有![]() ,解得
,解得![]() 或
或![]() 或
或![]() ,
,
故直线l的方程为﹣4x+y=0或﹣x+y+3=0或x+y+5=0;
(2)由直线l不经过第一象限,
则①当![]() ,即
,即![]() 时,直线l的方程为
时,直线l的方程为![]() ,显然满足题意;
,显然满足题意;
②当![]() ,即
,即![]() 时,则
时,则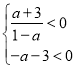 或
或![]() ,解得
,解得![]() ,
,
综合①②可得:实数a的取值范围为![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目