题目内容
4.已知函数f(x)=x3-$\frac{1}{2}$x2+bx+c.(1)若曲线y=f(x)在点 (1,f(1))处的切线方程为y=3x+$\frac{1}{2}$,分别求b,c的值.
(2)若f(x)在x=1时取得极值,且x∈[-1,2]时,f(x)<c2恒成立,求c的取值范围.
分析 (1)根据题可知:f(1)=$\frac{7}{2}$,f′(1)=3,列方程,求解
(2)求导,利用导函数求闭区间的最值,把恒成立问题转化为最值问题.
解答 解:(1)由题知:f(1)=$\frac{7}{2}$,f′(1)=3,f′(x)=3x2-x+b
∴b=1,c=2
(2)f′(x)=3x2-x+b
∵f(x)在x=1处取得极值
∴f′(1)=3-1+b=0
∴b=-2,
得f′(x)=3x2-x-2
∵当x∈[-1,2]时,f(x)<c2恒成立
∴x3-$\frac{1}{2}$x2-2x+c<c2在[-1,2]上恒成立
∴x3-$\frac{1}{2}$x2-2x<c2-c在[-1,2]上恒成立.
设h(x)=x3-$\frac{1}{2}$x2-2x
则h′(x)=3x2-x-2=(3x+2)(x-1)
当x∈(-1,-$\frac{2}{3}$)时,h′(x)>0
当x∈(-$\frac{2}{3}$,1)时,h′(x)<0
当x∈(1,2)时,h′(x)>0
∴当x=-$\frac{2}{3}$时,h(x)取得极大值为h(-$\frac{2}{3}$)=-$\frac{22}{27}$
h(2)=2
所以在[-1,2]上h(x)max=h(2)=2
则有c2-c>2,解得:c>2或c<-1
故c的取值范围为(-∞,-1)∪(2,+∞).
点评 考查了曲线上某点的切线的斜率等于该点的导数值;利用导数求闭区间上函数的最值,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的

练习册系列答案
相关题目
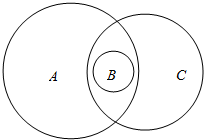 已知A={x|x具有性质p},B={x|x具有性质q},c={x|x具有性质r},集台A,B,C之间的关系如图所示:(注:每-个集合均是一个圆及其内部)
已知A={x|x具有性质p},B={x|x具有性质q},c={x|x具有性质r},集台A,B,C之间的关系如图所示:(注:每-个集合均是一个圆及其内部)