题目内容
【题目】已知抛物线
上一点
，点
，
是抛物线
上异于
的两动点，且
，则点到直线
的距离的最大值是______.
【答案】
【解析】
根据题意设出
,
的坐标和直线
的方程,将点坐标代入抛物线方程,联立直线与抛物线,结合平面向量数量积的坐标运算,由韦达定理即可求得直线的方程中
的等量关系式.进而求得直线所过定点
的坐标,结合点与直线的关系,即可知当
与直线垂直时点
到直线的距离最大,由两点间距离公式即可求解.
抛物线
,,是抛物线
上异于的两动点
设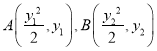
设直线的方程为
则
化简可得
所以
,
因为
则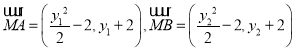
因为
所以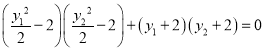
化简可得
所以
或
展开化简可得
或
代入可得
或
即
或
因为恒成立
当时,代入可得
,当
时
不恒成立,所以舍去
当时,代入可得
恒成立
所以
则直线的方程为
即
所以直线过定点
当与直线垂直时,点M到直线的距离最大,且最大距离为
故答案为:
【题目】某学校为鼓励家校互动,与某手机通讯商合作,为教师办理流量套餐.为了解该校教师手机流量使用情况,通过抽样,得到
位教师近
年每人手机月平均使用流量
(单位:
)的数据,其频率分布直方图如下：
若将每位教师的手机月平均使用流量分别视为其手机月使用流量,并将频率为概率,回答以下问题.
(Ⅰ) 从该校教师中随机抽取
人,求这人中至多有
人月使用流量不超过
的概率；
(Ⅱ) 现该通讯商推出三款流量套餐,详情如下:
套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位: |
|
|
|
|
|
|
|
|
|
这三款套餐都有如下附加条款:套餐费月初一次性收取,手机使用一旦超出套餐流量,系统就自动帮用户充值
流量,资费
元；如果又超出充值流量,系统就再次自动帮用户充值 流量,资费元/次,依次类推,如果当月流量有剩余,系统将自动清零,无法转入次月使用.
学校欲订购其中一款流量套餐,为教师支付月套餐费,并承担系统自动充值的流量资费的
,其余部分由教师个人承担,问学校订购哪一款套餐最经济？说明理由.
【题目】如图所示的数表为“森德拉姆筛”（森德拉姆，东印度学者），其特点是每行每列都成等差数列.在此表中，数字“121”出现的次数为___________.
2 | 3 | 4 | 5 | 6 | 7 | …… |
3 | 5 | 7 | 9 | 11 | 13 | …… |
4 | 7 | 10 | 13 | 16 | 19 | …… |
5 | 9 | 13 | 17 | 21 | 25 | …… |
6 | 11 | 16 | 21 | 26 | 31 | …… |
7 | 13 | 19 | 25 | 31 | 37 | …… |
…… | …… | …… | …… | …… | …… | …… |
