Question

【题目】一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛，每比赛一局商家要向每名棋手支付2000元对局费，同时商家每局从转让网络转播权及广告宣传中获利12100元，从两名棋手以往比赛中得知，甲每局获胜的概率为，乙每局获胜的概率为，两名棋手约定：最多下五局，先连胜两局者获胜，比赛结束，比赛结束后，商家为获胜者颁发5000元的奖金，若没有决出获胜者则各颁发2500元.

（1）求下完五局且甲获胜的概率是多少；

（2）求商家从这场网络棋赛中获得的收益的数学期望是多少.

Answer 1

【答案】（1）（2）

【解析】

（1）根据题意,连胜两局获胜.若比赛五局,且甲获胜,则五局的胜负情况为乙胜,甲胜,乙胜,甲胜,甲胜.进而由各自取胜的概率即可求解.

（2）根据题意可知,两人比赛局数可能的取值有.由所给取胜的概率,分别求得这四种情况下的概率,即可求得比赛局数的期望.扣除支出,即为商家获得的收益情况.

（1）根据题意,先连胜两局者获胜.则下完五局甲获胜,这五局的胜负情况分别为:

乙胜,甲胜,乙胜,甲胜,甲胜.

甲每局获胜的概率为,乙每局获胜的概率为

所以下完五局甲获胜的概率为

（2）设为比赛的局数,表示商家获得的收益

则

由题意可知,可能的取值有

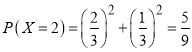
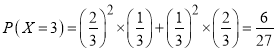
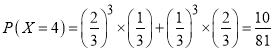
当比赛五局时,前四局两人各胜两局,且第五局无论谁胜商家都需支付5000元,因而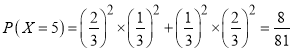

所以由离散型数学期望公式可得

故

所以商家从这场网络棋赛中获得的收益的数学期望是