题目内容
7.已知函数f(x)=2sin(x+$\frac{π}{3}$)+a的最大值为1(1)求常数a的值
(2)求使f(x)≥0成立的x的取值范围.
分析 (1)根据函数的最大值为1,得到2+a=1,即可求常数a的值
(2)根据三角函数的图象和性质解不等式f(x)≥0即可.
解答 解:(1)∵f(x)=2sin(x+$\frac{π}{3}$)+a的最大值为1,
∴当2sin(x+$\frac{π}{3}$)=1时,函数取得最大值为2+a=1,
即a=-1.
(2)∵a=-1,
∴f(x)=2sin(x+$\frac{π}{3}$)-1,
则由f(x)≥0得2sin(x+$\frac{π}{3}$)-1≥0,
即sin(x+$\frac{π}{3}$)≥$\frac{1}{2}$,
即2kπ+$\frac{π}{6}$≤x+$\frac{π}{3}$≤2kπ+$\frac{5π}{6}$,k∈Z,
即2kπ-$\frac{π}{6}$≤x≤2kπ+$\frac{π}{2}$,k∈Z,
即x的取值范围是[2kπ-$\frac{π}{6}$,2kπ+$\frac{π}{2}$],k∈Z.
点评 本题主要考查三角函数的图象和性质,利用正弦函数的有界性先求出a的值是解决本题的关键.

练习册系列答案
相关题目
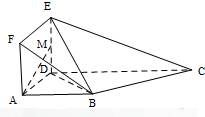 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.