题目内容
15.在等差数列{an}中,Sn为数列{an}的前n项和,满足a5=-1,S8=-12(1)求数列{an}的通项公式;
(2)求前n项和Sn,并指出当n为何值时,Sn取最小值;
(3)若Tn=|a1|+|a2|+…+|an|,求Tn.
分析 (1)通过联立a5=-1、S8=-12,计算即可;
(2)通过公式求和,结合二次函数的最值,计算即可;
(3)通过令an=n-6≥0得n≥6,分n≤5与n≥6两种情况计算即可.
解答 解:(1)∵${a_5}={a_1}+4d=-1,{S_8}=8{a_1}+\frac{8×7}{2}d=-12$,
∴a1=-5,d=1,
∴an=n-6;
(2)∵a1=-5,an=n-6,
∴${S_n}=\frac{{n({-5+n-6})}}{2}=\frac{1}{2}{n^2}-\frac{11}{2}n$,
而$\frac{1}{2}$n2-$\frac{11}{2}$n=$\frac{1}{2}$(n-$\frac{11}{2}$)2-$\frac{1}{2}•$$\frac{121}{4}$,
∵S5=$\frac{1}{2}•25-\frac{11}{2}•5$=-15,
S6=$\frac{1}{2}•36-\frac{11}{2}•6$=-15,
∴当n为5或6时,Sn取最小值;
(3)令an=n-6≥0,则n≥6,
$当n≤5时,{T_n}=-{a_1}-{a_2}-…-{a_n}=-{S_n}=-\frac{1}{2}{n^2}+\frac{11}{2}n$,
当n≥6时,Tn=-a1-a2-a3-a4-a5+a6+a7+…+an=$-2{S_5}+{S_n}=\frac{1}{2}{n^2}-\frac{11}{2}n+30$,
综上,${T_n}=\left\{\begin{array}{l}-\frac{1}{2}{n^2}+\frac{11}{2}n\;\;({n≤5})\\ \frac{1}{2}{n^2}-\frac{11}{2}n+30\;\;({n≥6})\end{array}\right.$.
点评 本题考查求数列的通项、求和及和的最值,考查运算求解能力,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $-\frac{12}{25}$ | B. | $\frac{7}{5}$ | C. | $\frac{1}{25}$ | D. | $-\frac{7}{25}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
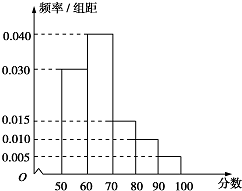 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.