题目内容
12.求函数y=-tan(2x-$\frac{3π}{4}$)的定义域{x|x≠$\frac{kπ}{2}$+$\frac{5π}{8}$,k∈Z}.分析 由题意可得2x-$\frac{3π}{4}$≠kπ+$\frac{π}{2}$,解不等式可得函数的定义域.
解答 解:由题意可得2x-$\frac{3π}{4}$≠kπ+$\frac{π}{2}$,
解得x≠$\frac{kπ}{2}$+$\frac{5π}{8}$,
∴函数的定义域为{x|x≠$\frac{kπ}{2}$+$\frac{5π}{8}$,k∈Z}
故答案为:{x|x≠$\frac{kπ}{2}$+$\frac{5π}{8}$,k∈Z}
点评 本题考查正切函数的定义域,属基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
20.已知α为第二象限角,$sinα+cosα=\frac{1}{5}$,则cos2α=( )
| A. | $-\frac{12}{25}$ | B. | $\frac{7}{5}$ | C. | $\frac{1}{25}$ | D. | $-\frac{7}{25}$ |
17.化简(x-4)4+4(x-4)3+6(x-4)2+4(x-4)+1得( )
| A. | x4 | B. | (x-3)4 | C. | (x+1)4 | D. | x5 |
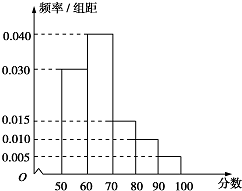 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.