Question

【题目】按照下列要求，分别求有多少种不同的方法？

（1）5个不同的小球放入3个不同的盒子；

（2）5个不同的小球放入3个不同的盒子，每个盒子至少一个小球；

（3）5个相同的小球放入3个不同的盒子，每个盒子至少一个小球；

（4）5个不同的小球放入3个不同的盒子，恰有1个空盒．

Answer 1

【答案】（1）243种（2）150种（3）6种（4）90种

【解析】

（1）利用分步乘法计数原理可求；

（2）先把5个小球分为三组，然后再放入三个盒中可得；

（3）利用隔板法进行求解，5个相同的小球，分成3组共有种方法；

（4）先把5个小球分为两组，然后再放入三个盒中可得.

（1）5个不同的小球放入3个不同的盒子，每个小球都有3种可能，利用乘法原理可得不同的方法有；

（2）5个不同的小球放入3个不同的盒子，每个盒子至少一个小球，先把5个小球分组，有两种分法：2、2、1；3、1、1；再放入3个不同的盒子，故不同的方法共有；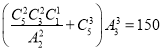

（3）5个相同的小球放入3个不同的盒子，每个盒子至少一个小球，类似于在5个小球间的空隙中，放入2个隔板，把小球分为3组，故不同的方法共有；

（4）5个不同的小球放入3个不同的盒子，恰有一个空盒，先把5个小球分2组，有两种分法：3、2、0；4、1、0；再放入3个不同的盒子，故不同的方法共有．