题目内容
如图所示,第 个图形是由正
个图形是由正 边形拓展而来(
边形拓展而来( ),则第
),则第 个图形共有____个顶点.
个图形共有____个顶点.

 个图形是由正
个图形是由正 边形拓展而来(
边形拓展而来( ),则第
),则第 个图形共有____个顶点.
个图形共有____个顶点.

试题分析:第一个图有
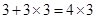 个顶点;
个顶点;第二个图有
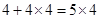 个顶点;
个顶点;第三个图有
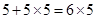 个顶点;
个顶点;第四个图有
 个顶点;
个顶点;…………………………………………
第
 个图有
个图有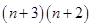 个顶点.
个顶点.第
 个图形共有
个图形共有 个顶点.
个顶点.
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
题目内容
 个图形是由正
个图形是由正 边形拓展而来(
边形拓展而来( ),则第
),则第 个图形共有____个顶点.
个图形共有____个顶点.

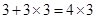 个顶点;
个顶点;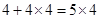 个顶点;
个顶点;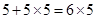 个顶点;
个顶点; 个顶点;
个顶点; 个图有
个图有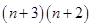 个顶点.
个顶点. 个图形共有
个图形共有 个顶点.
个顶点.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案