题目内容
如下图①②③④所示，它们都是由小圆圈组成的图案．现按同样的排列规则进行排列，记第
个图形包含的小圆圈个数为
，则（Ⅰ）
＝ ；（Ⅱ）
的个位数字为 ．
个图形包含的小圆圈个数为，则（Ⅰ）＝ ；（Ⅱ）的个位数字为 ．（Ⅰ）21；（Ⅱ）3
试题分析：（Ⅰ）
；
； 
；
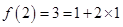；……由此可结纳出：
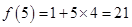.（Ⅱ）由（Ⅰ）
＝
；
＝
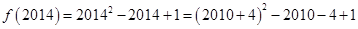
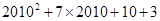.所以的个位数字是3.
练习册系列答案
快乐5加2金卷系列答案
相关题目
试题分析：（Ⅰ）
；； ；；……由此可结纳出：
.（Ⅱ）由（Ⅰ）
＝； ＝
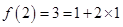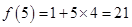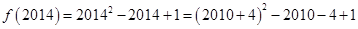
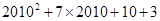.所以的个位数字是3.快乐5加2金卷系列答案
.
＋
＝1；
＋
＋
＋
＝12；
＋
＋
＋
＋
＋
＝39；
＋
＋
＋
＋…＋
＋
＝________(最后结果用m，n表示)．
个图形是由正
边形拓展而来（
），则第
个图形共有____个顶点．
(n∈N*)，经计算得f(4)＞2,f(8)＞
,f(16)＞3,f(32)＞
,……，观察上述结果，则可归纳出一般结论为 。
）；如果n是奇数，则将它乘3加1（即
），不断重复这样的运算，经过有限步后，一定可以得到1．如初始正整数为6，按照上述变换规则，我们可以得到一个数列：6，3，10，5，16，8，4，2，1．对于科拉茨猜想，目前谁也不能证明，也不能否定，现在请你研究：
，则按照上述规则施行变换后的第8项为 ．
（首项）按照上述规则施行变换后的第8项为1（注：1可以多次出现），则
则ak＋1＝( )．
－