题目内容
从0,1,2, ,10中挑选若干个不同的数字填满图中每一个圆圈称为一种“填法”,若各条线段相连的两个圆圈内的数字之差的绝对值各不相同,则称这样的填法为“完美填法”。
试问:对图1和图2是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由。
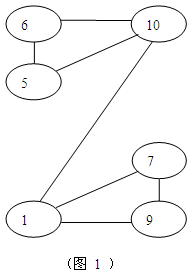
试问:对图1和图2是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由。


对图1,上述填法即为完美(答案不唯一)。
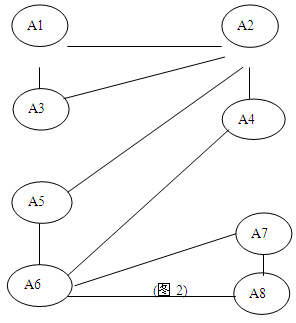
对于图2不存在完美填法。
对于图2不存在完美填法。
试题分析:对图1,上述填法即为完美(答案不唯一)。 10分
对于图2不存在完美填法。因为图中一共有10条连线,因此各连线上两数之差的绝对值恰好为,1,2,3, ,10, 15分
其和
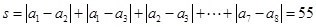 为奇数。 20分
为奇数。 20分另一方面,图中每一个圆圈所连接的连线数都为偶数条。即每一个圆圈内德数在上述S的表达式中出现偶数次。因此S应为偶数,矛盾。 25分
所以,不存在完美填法。
点评:难题,理解新定义内容是正确解题的关键。对图表的识别能力及转化与化归思想要求较高。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 个图形是由正
个图形是由正 边形拓展而来(
边形拓展而来( ),则第
),则第 个图形共有____个顶点.
个图形共有____个顶点.
 ,则在下列的一段推理过程中,错误的推理步骤有 .(填上所有错误步骤的序号)
,则在下列的一段推理过程中,错误的推理步骤有 .(填上所有错误步骤的序号)

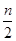 );如果n是奇数,则将它乘3加1(即
);如果n是奇数,则将它乘3加1(即 ),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:
),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究: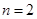 ,则按照上述规则施行变换后的第8项为 .
,则按照上述规则施行变换后的第8项为 . (首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则
(首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则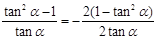
 =-
=-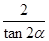 ①
①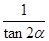 =-
=-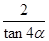 ②
②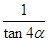 =-
=-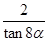 ③
③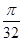 +2tan
+2tan +4tan
+4tan -
-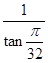 =( )
=( )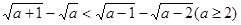 所用的最合适的方法是 .
所用的最合适的方法是 .