题目内容
(本小题10分)
当m取何值时,直线L:y=x+m与椭圆9x2+16y2=144相切、相交、相离.
当m取何值时,直线L:y=x+m与椭圆9x2+16y2=144相切、相交、相离.
解:将y=x+m代入9x2+16y2=144中,得
9x2+16(x+m)2=144.
整理,得25x2+32mx+16m2-144=0.
∵△=(32m)2-4·25·(16m2-144)=-576m2+14400,
∴当△>0,即-5<m<5时,直线L与椭圆相交.
当△=0,即m=土5时,直线L与椭圆相切.
当△<O,即m>5或m<-5时,直线L与椭圆相离.
9x2+16(x+m)2=144.
整理,得25x2+32mx+16m2-144=0.
∵△=(32m)2-4·25·(16m2-144)=-576m2+14400,
∴当△>0,即-5<m<5时,直线L与椭圆相交.
当△=0,即m=土5时,直线L与椭圆相切.
当△<O,即m>5或m<-5时,直线L与椭圆相离.
略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
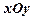 中,椭圆
中,椭圆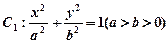 的左、右焦点分别为
的左、右焦点分别为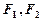 . 其中
. 其中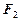 也是抛物线
也是抛物线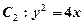 的焦点,点
的焦点,点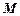 为
为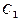 与
与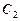 在第一象限的交点,且
在第一象限的交点,且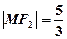
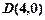 的直线
的直线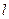 与
与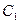 交于不同的两点
交于不同的两点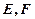 .
.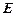 在
在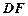 之间,试求
之间,试求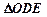 与
与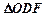 面积之比的取值范围.(O为坐标原点)
面积之比的取值范围.(O为坐标原点)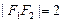
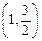 在椭圆C上.
在椭圆C上.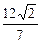 ,求以F2为圆
,求以F2为圆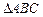 的两个顶点坐标分别是
的两个顶点坐标分别是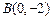 和
和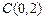 ,顶点A满足
,顶点A满足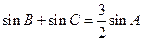 .
.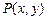 在(1)轨迹上,求
在(1)轨迹上,求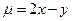 的最值.
的最值.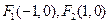 的椭圆经过点
的椭圆经过点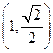 , 直线
, 直线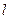 过点
过点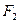 与椭圆交于
与椭圆交于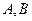 两点, 其中
两点, 其中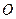 为坐标原点.
为坐标原点.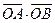 的范围;
的范围; 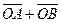 与向量
与向量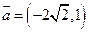 共线, 求
共线, 求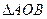 的外接圆方程.
的外接圆方程. 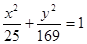 的焦点坐标是( )
的焦点坐标是( )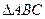 的顶点B、C在椭圆
的顶点B、C在椭圆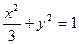 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则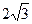 B. 6 C.
B. 6 C. 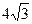 D. 12
D. 12 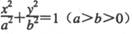 与直线
与直线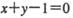 相交于A、B两点,且OA丄OB(O为坐标原点).
相交于A、B两点,且OA丄OB(O为坐标原点).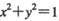 的交点坐标:
的交点坐标: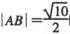 时,求椭圆E的方程.
时,求椭圆E的方程.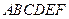 的两个顶点
的两个顶点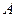 、
、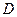 为椭圆的两个
为椭圆的两个