题目内容
(本小题满分12分)
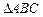 的两个顶点坐标分别是
的两个顶点坐标分别是 和
和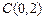 ,顶点A满足
,顶点A满足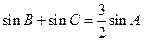 .
.
(1)求顶点A的轨迹方程;
(2)若点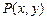 在(1)轨迹上,求
在(1)轨迹上,求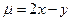 的最值.
的最值.
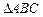 的两个顶点坐标分别是
的两个顶点坐标分别是 和
和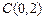 ,顶点A满足
,顶点A满足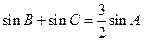 .
.(1)求顶点A的轨迹方程;
(2)若点
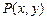 在(1)轨迹上,求
在(1)轨迹上,求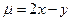 的最值.
的最值.解:(1)由正弦定理知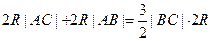

∴ …………(3分)
…………(3分)
∴A的轨迹是以B、C为焦点的椭圆,其中长短轴长 ,半焦距为
,半焦距为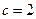
∴A的轨迹方程为 …………(6分)
…………(6分)
(2)法一
如图,当直线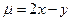 平移到
平移到 与椭圆相切时,
与椭圆相切时,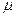 取最小,当直线
取最小,当直线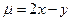 平移到
平移到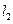 与椭圆相切时,
与椭圆相切时, 取最大, …………(8分)
取最大, …………(8分)

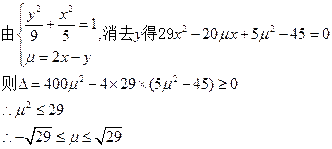
…………(11分)
当 时,
时, ,此时
,此时 不为最值
不为最值
∴ ,
,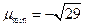 …………(12分)
…………(12分)
法二:P在(1)轨迹上,设 …………(7分)
…………(7分)
∴ …………(9分)
…………(9分)
(其中 )
)
∴ ,
,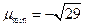 …………(11分)
…………(11分)
当 时,
时, ,此时
,此时 不为最值
不为最值
∴ ,
,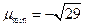 …………(12分)
…………(12分)
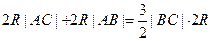

∴
 …………(3分)
…………(3分)∴A的轨迹是以B、C为焦点的椭圆,其中长短轴长
 ,半焦距为
,半焦距为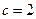
∴A的轨迹方程为
 …………(6分)
…………(6分)(2)法一
如图,当直线
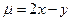 平移到
平移到 与椭圆相切时,
与椭圆相切时,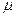 取最小,当直线
取最小,当直线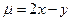 平移到
平移到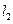 与椭圆相切时,
与椭圆相切时,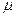 取最大, …………(8分)
取最大, …………(8分)
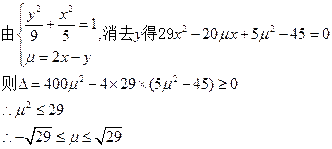
…………(11分)
当
 时,
时, ,此时
,此时 不为最值
不为最值∴
 ,
,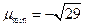 …………(12分)
…………(12分)法二:P在(1)轨迹上,设
 …………(7分)
…………(7分)∴
 …………(9分)
…………(9分)(其中
 )
)∴
 ,
,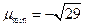 …………(11分)
…………(11分)当
 时,
时, ,此时
,此时 不为最值
不为最值∴
 ,
,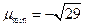 …………(12分)
…………(12分)略

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

 是椭圆
是椭圆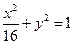 的内接△
的内接△ 的内切圆, 其中
的内切圆, 其中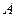 为椭圆的左顶点.
为椭圆的左顶点.
 的半径
的半径 ;
; 2)过点
2)过点 作圆
作圆 两点,
两点, 与圆
与圆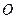 ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线 交椭圆于
交椭圆于 ,
,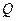 两点.
两点. 的面积;
的面积; 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线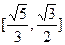
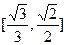
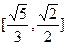

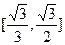

 及椭圆
及椭圆 的实线部分上运动,且AB∥Y轴,则
的实线部分上运动,且AB∥Y轴,则 的周长的取值范围是( )
的周长的取值范围是( )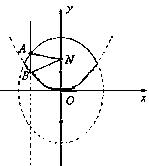




 (a>b>0)的
(a>b>0)的 离心率为
离心率为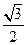 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若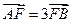 。则
。则 ( )
( ) 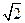 (D)
(D)
 :方程
:方程 表示焦点在
表示焦点在 轴上的椭圆,命题
轴上的椭圆,命题 :关于x的方程
:关于x的方程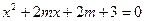 无实根,若“
无实根,若“ ”为假命题,“
”为假命题,“ ”为真命题,求实数
”为真命题,求实数 的取值范围.
的取值范围. 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则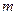 的取值范围是_____
的取值范围是_____