题目内容
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
(1)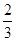 (2)
(2)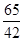
解析

练习册系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
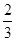 .
.(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
| P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=
 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=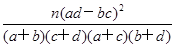 ,其中n=a+b+c+d)
,其中n=a+b+c+d) 某公司研制出一种新型药品,为测试该药品的有效性,公司选定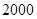 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:
| 分组 | 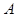 组 组 | 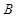 组 组 |  组 组 |
| 药品有效 | 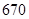 | 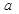 | 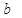 |
| 药品无效 | 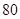 | 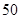 | 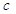 |
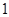 个,抽到
个,抽到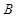 组药品有效的概率是
组药品有效的概率是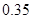 .
.(1)现用分层抽样的方法在全体样本中抽取
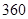 个测试结果,问应在
个测试结果,问应在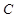 组抽取样本多少个? [来源:学优]
组抽取样本多少个? [来源:学优](2)已知
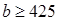 ,
,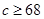 ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于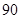 %,则认为测试通过).
%,则认为测试通过). 为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为
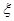 ,求随机变量
,求随机变量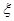 的分布列,及数学期望.
的分布列,及数学期望.  ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立. π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率. 表示.
表示.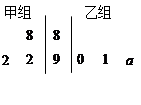
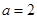 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为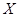 ,求随机变量
,求随机变量 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.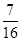 ,求走公路②堵车的概率;
,求走公路②堵车的概率;