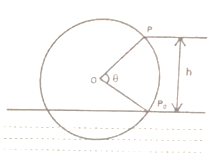
题目内容
【题目】给出下列三个等式:f(x+y)=f(x)f(y),f(xy)=f(x)+f(y),f(ax+by)=af(x)+bf(y)(a+b=1).下列选项中,不满足其中任何一个等式的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
依据指数函数、对数函数的性质可以发现A,C满足其中的一个等式,而B满足f(ax+by)=af(x)+bf(y)(a+b=1),D不满足其中任何一个等式.
f(x)=3x是指数函数,有3x+y=3x3y,满足f(x+y)=f(x)f(y),排除A;
f(x)=log2x是对数函数,有log2(xy)=log2x+log2y,满足f(xy)=f(x)+f(y),排除C;
f(x)=4-x为一次函数,有4-(ax+by)=a(4-x)+b(4-y)(a+b=1),
满足f(ax+by)=af(x)+bf(y)(a+b=1),排除B.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目