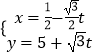��Ŀ����
����Ŀ����֪����{an}��ǰn���ΪSn �� ����Sn=2an��1��n��N*������{bn}����nbn+1����n+1��bn=n��n+1����n��N*����b1=1��
��1��������{an}��{bn}��ͨ�ʽ��
��2����cn=an ![]() ������{cn}��ǰn���ΪTn �� �������n��N*������Tn��nSn��a����ʵ��a��ȡֵ��Χ��
������{cn}��ǰn���ΪTn �� �������n��N*������Tn��nSn��a����ʵ��a��ȡֵ��Χ��
��3���Ƿ����������m��nʹb1 �� am �� bn��n��1���ɵȲ����У������ڣ������������������m��n���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��n=1ʱ��S1=2a1��1=a1������a1=1��
��n��2ʱ��Sn=2an��1��Sn��1=2an��1��1��
��ʽ�����an=2an��1��
�Ӷ�����{an}Ϊ����a1=1������q=2�ĵȱ����У�
�Ӷ�����{an}��ͨ�ʽΪan=2n��1��
��nbn+1����n+1��bn=n��n+1��������ͬ����n��n+1����
�� ![]() ��
�� ![]() =1��
=1��
�Ӷ�����{ ![]() }Ϊ����b1=1������d=1�ĵȲ����У�����
}Ϊ����b1=1������d=1�ĵȲ����У����� ![]() =n��
=n��
�Ӷ�����{bn}��ͨ�ʽΪbn=n2
��2���⣺�ɣ�1����cn=an ![]() =n2n��1��
=n2n��1��
����Tn=1��1+2��2+3��22+��+��n��1��2n��2+n2n��1��
����2Tn=1��21+2��22+3��23+��+��n��1��2n��1+n2n��
��ʽ����é�Tn=1+21+22+23+��+2n��1��n2n= ![]() ��n��2n��
��n��2n��
����Tn=��n��1��2n+1
�ɣ�1����Sn=2an��1=2n��1��
�������n��N*������Tn��nSn��a��
����n��1��2n+1��n��2n��1����a�������
����a��2n��n��1�������
��cn=2n��n��1��
����a����cn��min��
��Ϊ ![]() =2n��1��0��
=2n��1��0��
�Ӷ�����{cn}Ϊ�������У����Ե�n=1ʱcnȡ��Сֵc1=0��
����a��0
��3���⣺�������������m��n��n��1����ʹb1��am��bn�ɵȲ����У���b1+bn=2am��
��1+n2=2m��
��nΪż������1+n2Ϊ��������2mΪż������ʽ��������
��n��������n=2k��1��k��N*������1+n2=1+��2k��1��2=4k2��4k+2=2m��
����2k2��2k+1=2m��1����2��k2��k��+1=2m��1��
��m=1ʱ��k=1����ʱn=2k��1=1��n��1ì�ܣ�
��m��2ʱ����ʽ���Ϊ�������ұ�Ϊż������Ȼ��������
��������������������ʵ���ԣ�m��n��������
����������1������Sn���� an �Ĺ�ϵ��������е�ͨ�ʽ��������֪�����ɵ�����{ ![]() }ʱ����b1=1������d=1�ĵȲ����У������ó�����{bn}��ͨ�ʽ����2�������������ó��Թ�����������ɵõ�Tn=��n��1��2n+1���ٸ�����֪�õ���n��1��2n+1��n��2n��1����a�������a��2n��n��1�������֤���õ�����{cn}Ϊ�������У����Ե�n=1ʱcnȡ��Сֵc1=0���õ�a��ȡֵ��Χ����3��������ڸ��������жϵõ���nΪż����ʽ����������nΪ������2��k2��k��+1=2m��1���Դ�ʽ�ӽ��з����õ�����������������������ʵ���ԣ�m��n�������ڡ�
}ʱ����b1=1������d=1�ĵȲ����У������ó�����{bn}��ͨ�ʽ����2�������������ó��Թ�����������ɵõ�Tn=��n��1��2n+1���ٸ�����֪�õ���n��1��2n+1��n��2n��1����a�������a��2n��n��1�������֤���õ�����{cn}Ϊ�������У����Ե�n=1ʱcnȡ��Сֵc1=0���õ�a��ȡֵ��Χ����3��������ڸ��������жϵõ���nΪż����ʽ����������nΪ������2��k2��k��+1=2m��1���Դ�ʽ�ӽ��з����õ�����������������������ʵ���ԣ�m��n�������ڡ�

 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�