题目内容
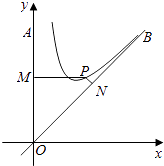
【题目】已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若 ![]() ,其中m,n∈R.则m+n的取值范围是( )
,其中m,n∈R.则m+n的取值范围是( )
A.(0,1)
B.(﹣1,0)
C.(1,+∞)
D.(﹣∞,﹣1)
【答案】B
【解析】解:∵|OC|=|OB|=|OA|, ![]() ,
,
∴1=m2+n2+2mncos∠AOB
当∠AOB=60°时,m2+n2+mn=1,m<0,n>0,即(m+n)2﹣mn=1,即(m+n)2=1+mn<1,
所以(m+n)2<1,
∴﹣1<m+n<1,当 ![]() ,
, ![]() 趋近射线OD,
趋近射线OD,
由平行四边形法则 ![]() =
= ![]() +
+ ![]() =m
=m ![]() +n
+n ![]() ,此时显然m<0,n>0,且|m|>|n|,
,此时显然m<0,n>0,且|m|>|n|,
∴m+n<0,所以m+n的取值范围(﹣1,0).
故选B.

【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案,需要熟知如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
相关题目
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.