题目内容
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,M、N分别是棱AB、CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
①平面MB1P⊥ND1;②平面MB1P⊥平面ND1A1;③△MB1P在底面ABCD上的射影图形的面积为定值;④△MB1P在侧面D1C1CD上的射影图形是三角形.
其中正确命题的序号是 . 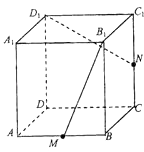
【答案】②③
【解析】解:①平面MB1P⊥ND1;可用极限位置判断,当P与N重合时,MB1P⊥ND1垂直不成立,故线面不可能垂直,此命题是错误命题;
②平面MB1P⊥平面ND1A1;可以证明MB1⊥平面ND1A1,由图形知MB1与ND1和D1A1都垂直,故可证得MB1⊥平面ND1A1,进而可得平面MB1P⊥平面ND1A1,故是正确命题;
③△MB1P在底面ABCD上的射影图形的面积为定值,可以看到其投影三角形底边是MB,再由点P在底面上的投影在DC上,故其到MB的距离不变即可证得;
④△MB1P在侧面D1C1CD上的射影图形是三角形,由于P与C1重合时,P、B1两点的投影重合,不能构成三角形,故命题错误.
综上②③正确
所以答案是:②③.
【考点精析】本题主要考查了平面与平面之间的位置关系的相关知识点,需要掌握两个平面平行没有交点;两个平面相交有一条公共直线才能正确解答此题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目