题目内容
【题目】已知直线l的参数方程为  为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .直线l过点
.直线l过点 ![]() .
.
(1)若直线l与曲线C交于A,B两点,求 ![]() 的值;
的值;
(2)求曲线C的内接矩形的周长的最大值.
【答案】
(1)解:已知曲线C的标准方程为 ![]() ,则其左焦点为
,则其左焦点为 ![]() ,则
,则 ![]() ,将直线l的参数方程
,将直线l的参数方程 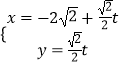 与曲线C的方程
与曲线C的方程 ![]() 联立,得
联立,得 ![]() ,则
,则 ![]() .
.
(2)解:由曲线C的方程为 ![]() ,可设曲线C上的动点
,可设曲线C上的动点 ![]() ,则以P为顶点的内接矩形周长为
,则以P为顶点的内接矩形周长为 ![]() ,因此该内接矩形周长的最大值为16
,因此该内接矩形周长的最大值为16
【解析】(1)先将曲线C的极坐标方程化为直角坐标方程,再将直线的参数方程代入得到参数t的一雹二次方程,结合t的几何意义求出 | F A | | F B|的值。
(2)根据对称性由参数方程设出椭圆的内接矩形其中一个顶点的坐标,得到目标周长关于参数角![]() 的函数式,利用三角函数知识求最值。
的函数式,利用三角函数知识求最值。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目