题目内容
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() ,
,![]() 是
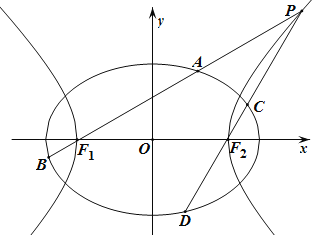
是![]() 右支上的一点,
右支上的一点,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 的内切圆在边
的内切圆在边![]() 上的切点为
上的切点为![]() .若
.若![]() ,则
,则![]() 的离心率是________.
的离心率是________.
【答案】![]()
【解析】
由双曲线的定义和内切圆的切线性质:圆外一点向圆引切线,则切线长相等,结合离心率公式即可得到所求值.
设△PAF2的内切圆在边PF2上的切点为M,在AP上的切点为N,
则|PM|=|PN|,|AQ|=|AN|![]() ,|QF2|=|MF2|,
,|QF2|=|MF2|,
由双曲线的对称性可得|AF1|=|AF2|=|AQ|+|QF2|![]() |QF2|,
|QF2|,
由双曲线的定义可得|PF1|﹣|PF2|=|PA|+|AF1|﹣|PM|﹣|MF2|
![]() |QF2|+|AN|+|NP|﹣|PM|﹣|MF2|
|QF2|+|AN|+|NP|﹣|PM|﹣|MF2|
=4![]() 2a,解得a
2a,解得a![]() ,
,
又|F1F2|=6,即有c=3,
离心率e![]() .
.
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目