题目内容
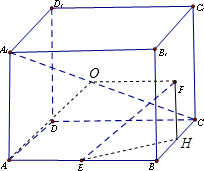
如图,正方体ABCD-A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.
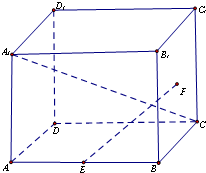
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.

解法一:(1)取BC中点H,连结FH,EH,设正方体棱长为2.
∵F为BCC1B1中心,E为AB中点.
∴FH⊥平面ABCD,FH=1,EH=
.
∴∠FEH为直线EF与平面ABCD所成角,且FH⊥EH.
∴tan∠FEH=
=
=
.…(6分)
(2)取A1C中点O,连接OF,OA,则OF∥AE,且OF=AE.
∴四边形AEFO为平行四边形.∴AO∥EF.
∴∠AOA1为异面直线A1C与EF所成角.
∵A1A=2,AO=A1O=
.
∴△AOA1中,由余弦定理得cos∠A1OA=
.…(12分)
解法二:设正方体棱长为2,以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系.则B(0,0,0),B1(0,0,2),E(0,1,0),F(1,0,1),C(2,0,0),A1(0,2,2).
(1)
=(1,-1,1),
=(0,0,2),且
为平面ABCD的法向量.
∴cos<
,
>=
.
设直线EF与平面ABCD所成角大小为θ.
∴sinθ=
,从而tanθ=
.…(6分)
(2)∵
=(2,-2,-2),∴cos<
,
>=
.
∴异面直线A1C与EF所成角的余弦值为
.…(12分)
∵F为BCC1B1中心,E为AB中点.
∴FH⊥平面ABCD,FH=1,EH=
| 2 |
∴∠FEH为直线EF与平面ABCD所成角,且FH⊥EH.
∴tan∠FEH=
| FH |
| EH |
| 1 | ||
|
| ||
| 2 |
(2)取A1C中点O,连接OF,OA,则OF∥AE,且OF=AE.
∴四边形AEFO为平行四边形.∴AO∥EF.
∴∠AOA1为异面直线A1C与EF所成角.
∵A1A=2,AO=A1O=
| 3 |
∴△AOA1中,由余弦定理得cos∠A1OA=
| 1 |
| 3 |
解法二:设正方体棱长为2,以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系.则B(0,0,0),B1(0,0,2),E(0,1,0),F(1,0,1),C(2,0,0),A1(0,2,2).
(1)
| EF |
| BB1 |
| BB1 |

∴cos<
| EF |
| BB1 |
| ||
| 3 |
设直线EF与平面ABCD所成角大小为θ.
∴sinθ=
| ||
| 3 |
| ||
| 2 |
(2)∵
| A1C |
| CA1 |
| EF |
| 1 |
| 3 |
∴异面直线A1C与EF所成角的余弦值为
| 1 |
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目