题目内容
【题目】已知函数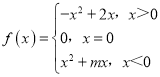 是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有
是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立,则实数a的取值范围是______.
成立,则实数a的取值范围是______.
【答案】2 1<a≤3
【解析】
f(x)为奇函数,有f(-x)=-f(x),可计算出m的值为2,;函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立,即函数f(x)在[-1,2]上为增函数,由函数f(x)在[-1,1]单调增,则[-1,a-2] [-1,1],得1<a≤3;
成立,即函数f(x)在[-1,2]上为增函数,由函数f(x)在[-1,1]单调增,则[-1,a-2] [-1,1],得1<a≤3;
f(x)为奇函数,则f(-x)=-f(x);
所以f(-1)=1-m=-(-1+2)=-1,则m=2;
函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立;
成立;
则函数f(x)在[-1,a-2]上为增函数,且![]()
又函数f(x)的增区间为[-1,1];则[-1,a-2] [-1,1]得1<a≤3;
故答案为:2,1<a≤3;

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)若![]() ,求
,求![]() 的值.
的值.