Question

在平面直角坐标系中，平面区域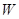中的点的坐标满足，从区域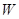中随机取点．
（Ⅰ）若，，求点位于第四象限的概率；
（Ⅱ）已知直线与圆相交所截得的弦长为，求的概率．

Answer 1

（Ⅰ）；（Ⅱ）。

解析试题分析：（Ⅰ）若，，则点的个数共有个，列举如下：
；；
；；
 ．
当点的坐标为时，点位于第四象限．
故点位于第四象限的概率为．
（Ⅱ）由已知可知区域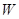的面积是．

因为直线与圆的弦长为，如图，可求得扇形的圆心角为，所以扇形的面积为，则满足的点构成的区域的面积为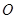

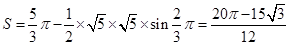，所以的概率为．

考点：古典概型；几何概型；扇形的面积公式。
点评：注意古典还行与几何概型的区别：。古典概型：试验中所有可能出现的基本事件只有有限个；几何概型：试验中所有可能出现的基本事件有无限多个。