题目内容
甲、乙等五名奥运志愿者被随机地分到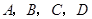 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加
四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量
岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,
岗位服务的人数,  可取何值?请求出相应的
可取何值?请求出相应的 值的分布列.
值的分布列.
(Ⅰ)甲、乙两人同时参加 岗位服务的概率是
岗位服务的概率是 . (Ⅱ)甲、乙两人不在同一岗位服务的概率是
. (Ⅱ)甲、乙两人不在同一岗位服务的概率是 .(Ⅲ)随机变量
.(Ⅲ)随机变量 可能取的值为1,2.
可能取的值为1,2.  .
. 
解析试题分析:(Ⅰ)记甲、乙两人同时参加 岗位服务为事件
岗位服务为事件 ,那么
,那么 ,即甲、乙两人同时参加
,即甲、乙两人同时参加 岗位服务的概率是
岗位服务的概率是 . 4分
. 4分
(Ⅱ)记甲、乙两人同时参加同一岗位服务为事件 ,那么
,那么 ,所以,甲、乙两人不在同一岗位服务的概率是
,所以,甲、乙两人不在同一岗位服务的概率是 . 8分
. 8分
(Ⅲ)随机变量 可能取的值为1,2.事件“
可能取的值为1,2.事件“ ”是指有两人同时参加
”是指有两人同时参加 岗位服务,则
岗位服务,则 .所以
.所以 12分
12分
考点:本题考查了随机事件的概率及分布列的定义
点评:熟练掌握随机变量的取值及分布列的概念是解决此类问题的关键,属常考题型

练习册系列答案
相关题目
 ,
, ,
, ,
, ,
, ,
, .
. ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响. ,求
,求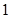 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响. 局结束,且乙比甲多得
局结束,且乙比甲多得 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望;
的分布列和数学期望; (
(
 )
) 从集合
从集合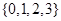 中任取一个元素,
中任取一个元素, 从集合
从集合 恰有两个不相等实根的概率;
恰有两个不相等实根的概率; 中任取一个数,
中任取一个数, 中任取一个数,求方程
中任取一个数,求方程