题目内容
5.已知f(x)=$\frac{a{x}^{2}+1}{bx+c}$(a,b,c∈Z)满足f(-x)+f(x)=0,且f(1)=2,f(2)<3.(1)求a,b,c的值;
(2)当x≤-1时,判断f(x)的单调性.
分析 (1)根据f(-x)+f(x)=0可得出c=0,而根据f(1)=2可以得到b=$\frac{a+1}{2}$,此时便可得出f(x)=$\frac{a{x}^{2}+1}{\frac{a+1}{2}x}$,再根据条件f(2)<3可得到a的范围,而根据a,b∈Z便可得出a=b=1;
(2)由上面可得出f(x)=$x+\frac{1}{x}$,求导,判断导数f′(x)在x≤-1时的符号,即可判断出f(x)的单调性.
解答 解:(1)由f(-x)+f(x)=0得,f(-x)=-f(x);
∴$\frac{a{x}^{2}+1}{-bx+c}=\frac{a{x}^{2}+1}{-bx-c}$;
∴-bx+c=-bx-c;
∴c=0;
∴由f(1)=2得,$\frac{a+1}{b}=2$,即b=$\frac{a+1}{2}$;
∴f(x)=$\frac{a{x}^{2}+1}{\frac{a+1}{2}x}$;
f(2)<3;
∴$\frac{4a+1}{a+1}<3$;
解得-1<a<2,又a,b∈Z;
∴a=1,b=1;
∴a,b,c的值分别为1,1,0;
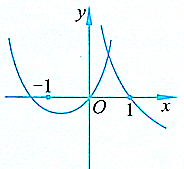
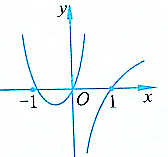
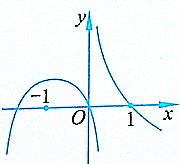
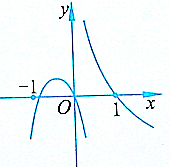
(2)f(x)=$\frac{{x}^{2}+1}{x}$=x$+\frac{1}{x}$;
∴$f′(x)=\frac{{x}^{2}-1}{{x}^{2}}$;
∵x≤-1;
∴x2-1≥0;
∴f′(x)≥0;
∴当x≤-1时,f(x)单调递增.
点评 考查奇函数的定义,通过条件求函数f(x)解析式中的参数,从而确定函数解析式的方法,注意条件a,b为整数的运用,以及根据导数符号判断函数单调性的方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.下列式子中,y不是x的函数的是( )
| A. | x=y2+1 | B. | y=2x2+1 | C. | x-2y=6 | D. | x=$\sqrt{y}$ |
14.下列不等式中,解集是一切实数的是( )
| A. | 4x2-4x+1>0 | B. | -x2+x-4<0 | C. | x2-2x+3<0 | D. | x2-x-2>0 |