题目内容
(本题满分14分) 设函数f (x)=ln x+ 在(0,
在(0, ) 内有极值.
) 内有极值.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+ ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2- .
.
注:e是自然对数的底数.
 在(0,
在(0, ) 内有极值.
) 内有极值.(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+
 ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2- .
.注:e是自然对数的底数.
(Ⅰ)解: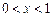 或
或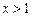 时,
时,
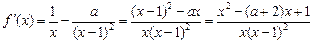 .
.
由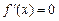 在
在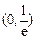 内有解.令
内有解.令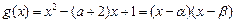 ,
,
不妨设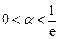 ,则
,则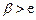 ,所以
,所以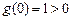 ,
,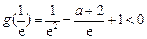 ,
,
解得 .
.
(Ⅱ)解:由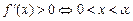 或
或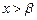 ,
,
由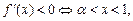 ,或
,或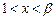 ,
,
得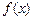 在
在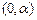 内递增,在
内递增,在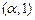 内递减,在
内递减,在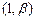 内递减,在
内递减,在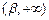 递增.
递增.
由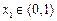 ,得
,得 ,
,
由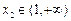 得
得 ,
,
所以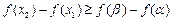 ,
,
因为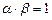 ,
,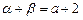 ,
,
所以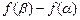

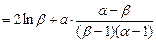
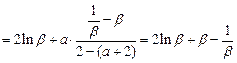 ,
,
记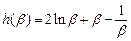 , (
, (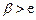 ),
),
则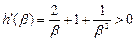 ,
, 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
所以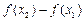
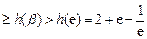 .
.
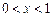 或
或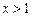 时,
时,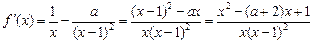 .
.由
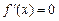 在
在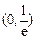 内有解.令
内有解.令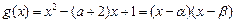 ,
,不妨设
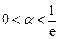 ,则
,则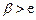 ,所以
,所以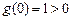 ,
,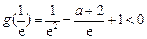 ,
,解得
 .
. (Ⅱ)解:由
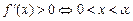 或
或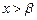 ,
,由
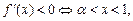 ,或
,或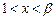 ,
,得
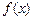 在
在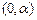 内递增,在
内递增,在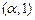 内递减,在
内递减,在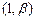 内递减,在
内递减,在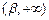 递增.
递增.由
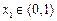 ,得
,得 ,
,由
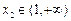 得
得 ,
,所以
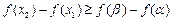 ,
,因为
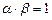 ,
,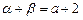 ,
,所以
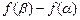

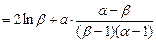
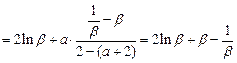 ,
,记
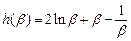 , (
, (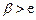 ),
),则
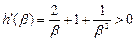 ,
, 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,所以
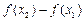
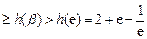 .
. 略

练习册系列答案
相关题目
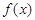 对于任意
对于任意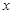 ,有
,有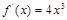 ,
,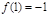 ,则此函数为( )
,则此函数为( )
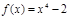


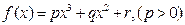 图象的对称中心为
图象的对称中心为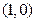 ,且
,且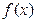 的极小值为
的极小值为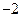 .
.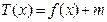 ,若
,若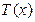 有三个零点,求实数
有三个零点,求实数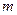 的取值范围;
的取值范围;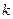 ,当
,当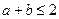 时,使函数
时,使函数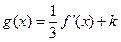
 ,
,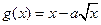 ,且
,且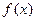 在
在 处取极值。
处取极值。 的单调性。
的单调性。 时,恒有
时,恒有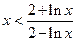 成立.
成立. .
. ,讨论
,讨论 的单调性;
的单调性; 恒有
恒有 ,求
,求 的取值范围.
的取值范围. 的导数是
的导数是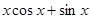



 在区间
在区间 上是减函数,则
上是减函数,则 的最小值是( )
的最小值是( )


 (
( ,c为常数且1《c《4)的导函数的图象如图所示:
,c为常数且1《c《4)的导函数的图象如图所示:
 1).求
1).求 ,求
,求 在
在 上的最大值
上的最大值 。
。 ,那么
,那么 .
.