题目内容
(本题满分14分)
定义在(0,+∞)上的函数 ,
,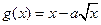 ,且
,且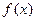 在
在 处取极值。
处取极值。
(Ⅰ)确定函数 的单调性。
的单调性。
(Ⅱ)证明:当 时,恒有
时,恒有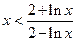 成立.
成立.
定义在(0,+∞)上的函数
 ,
,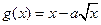 ,且
,且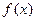 在
在 处取极值。
处取极值。(Ⅰ)确定函数
 的单调性。
的单调性。(Ⅱ)证明:当
 时,恒有
时,恒有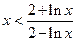 成立.
成立.解:(Ⅰ) ,则
,则 ,
,
由已知 ,即
,即 . …………3分
. …………3分
所以 ,则
,则 .由
.由 ,…………5分
,…………5分
所以 在
在 上是增函数,在
上是增函数,在 上是减函数. …………6分
上是减函数. …………6分
(Ⅱ) 当 时,
时,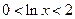 ,要证
,要证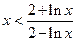 等价于
等价于
 ,即
,即
设 ,则
,则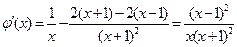 . ……10分
. ……10分
当 时,
时,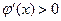 ,所以
,所以 在区间(1,e2)上为增函数. ……12分
在区间(1,e2)上为增函数. ……12分
从而当 时,
时, ,即
,即 ,故
,故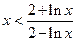 ……14分。
……14分。
 ,则
,则 ,
,由已知
 ,即
,即 . …………3分
. …………3分所以
 ,则
,则 .由
.由 ,…………5分
,…………5分 所以
 在
在 上是增函数,在
上是增函数,在 上是减函数. …………6分
上是减函数. …………6分(Ⅱ) 当
 时,
时,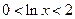 ,要证
,要证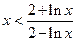 等价于
等价于 ,即
,即
设
 ,则
,则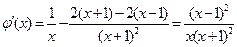 . ……10分
. ……10分 当
 时,
时,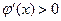 ,所以
,所以 在区间(1,e2)上为增函数. ……12分
在区间(1,e2)上为增函数. ……12分 从而当
 时,
时, ,即
,即 ,故
,故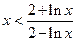 ……14分。
……14分。略

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
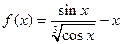
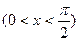 .
.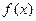 的导数
的导数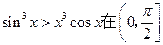 上恒成立;
上恒成立;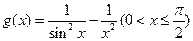 的最大值.
的最大值. 在(0,
在(0, ) 内有极值.
) 内有极值. ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2-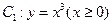 与曲线
与曲线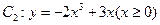 交于点
交于点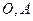 .直线
.直线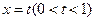 与曲线
与曲线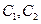 分别相交于点
分别相交于点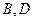 .
.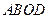 的面
的面 积
积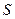 与
与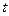 的函数关系
的函数关系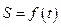 ;
;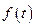 的单调性,并求
的单调性,并求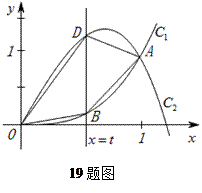
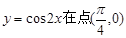 处的切线方程是 ( )
处的切线方程是 ( ) 在点
在点 处的切线方程为
处的切线方程为  (x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。
(x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。 (1)若
(1)若
 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围; (2)若
的取值范围; (2)若 是
是 上的最大值;(3)在(2)的条件下,是否存在实数
上的最大值;(3)在(2)的条件下,是否存在实数 ,使得函数
,使得函数 的图像与函数
的图像与函数