题目内容
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
【答案】
(1)
解:∵f(x)=|x+1|﹣|x﹣2|= 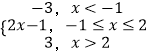 ,f(x)≥1,
,f(x)≥1,
∴当﹣1≤x≤2时,2x﹣1≥1,解得1≤x≤2;
当x>2时,3≥1恒成立,故x>2;
综上,不等式f(x)≥1的解集为{x|x≥1}.
(2)
原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,
即m≤[f(x)﹣x2+x]max,设g(x)=f(x)﹣x2+x.
由(1)知,g(x)=  ,
,
当x≤﹣1时,g(x)=﹣x2+x﹣3,其开口向下,对称轴方程为x= ![]() >﹣1,
>﹣1,
∴g(x)≤g(﹣1)=﹣1﹣1﹣3=﹣5;
当﹣1<x<2时,g(x)=﹣x2+3x﹣1,其开口向下,对称轴方程为x= ![]() ∈(﹣1,2),
∈(﹣1,2),
∴g(x)≤g( ![]() )=﹣
)=﹣ ![]() +
+ ![]() ﹣1=
﹣1= ![]() ;
;
当x≥2时,g(x)=﹣x2+x+3,其开口向下,对称轴方程为x= ![]() <2,
<2,
∴g(x)≤g(2)=﹣4+2=3=1;
综上,g(x)max= ![]() ,
,
∴m的取值范围为(﹣∞, ![]() ].
].
【解析】(1.)由于f(x)=|x+1|﹣|x﹣2|= 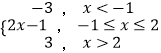 ,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
(2.)依题意可得m≤[f(x)﹣x2+x]max , 设g(x)=f(x)﹣x2+x,分x≤1、﹣1<x<2、x≥2三类讨论,可求得g(x)max= ![]() ,从而可得m的取值范围.
,从而可得m的取值范围.
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,以及对绝对值不等式的解法的理解,了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

【题目】“红灯停,绿灯行”,这是我们每个人都应该也必须遵守的交通规则.凑齐一拨人就过马路﹣﹣不看交通信号灯、随意穿行交叉路口的“中国式过马路”不仅不文明而且存在很大的交通安全隐患.一座城市是否存在“中国式过马路”是衡量这座城市文明程度的重要指标.某调查机构为了了解路人对“中国式过马路”的态度,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此列联表数据判断是否有95%的把握认为反感“中国式过马路”与性别有关?
(2)若从这30人中的女性路人中随机抽取2人参加一项活动,记反感“中国式过马路”的人数为X,求X的分布列及其数学期望.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |