题目内容
(2013•浙江)△ABC中,∠C=90°,M是BC的中点,若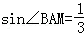 ,则sin∠BAC= _________ .
,则sin∠BAC= _________ .
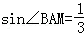 ,则sin∠BAC= _________ .
,则sin∠BAC= _________ .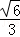
如图
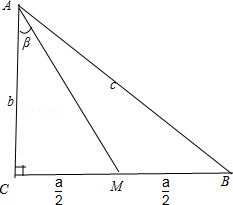
设AC=b,AB=c,CM=MB=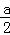 ,∠MAC=β,
,∠MAC=β,
在△ABM中,由正弦定理可得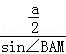 =
=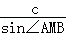 ,
,
代入数据可得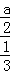 =
=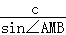 ,解得sin∠AMB=
,解得sin∠AMB=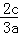 ,
,
故cosβ=cos(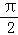 ﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=
﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=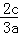 ,
,
而在RT△ACM中,cosβ=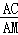 =
=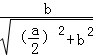 ,
,
故可得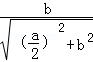 =
=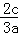 ,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,
,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,
解之可得a=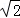 b,再由勾股定理可得a2+b2=c2,联立可得c=
b,再由勾股定理可得a2+b2=c2,联立可得c=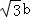 ,
,
故在RT△ABC中,sin∠BAC=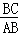 =
=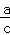 =
=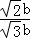 =
=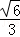 ,
,
故答案为: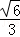

设AC=b,AB=c,CM=MB=
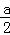 ,∠MAC=β,
,∠MAC=β,在△ABM中,由正弦定理可得
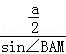 =
=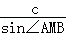 ,
,代入数据可得
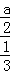 =
=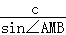 ,解得sin∠AMB=
,解得sin∠AMB=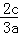 ,
,故cosβ=cos(
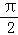 ﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=
﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=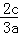 ,
,而在RT△ACM中,cosβ=
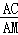 =
=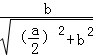 ,
,故可得
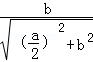 =
=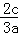 ,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,
,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,解之可得a=
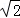 b,再由勾股定理可得a2+b2=c2,联立可得c=
b,再由勾股定理可得a2+b2=c2,联立可得c=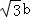 ,
,故在RT△ABC中,sin∠BAC=
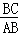 =
=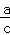 =
=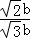 =
=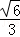 ,
,故答案为:

练习册系列答案
相关题目
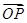 =
=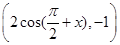 ,
,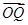 =
=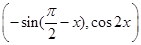 ,定义函数f(x)=
,定义函数f(x)=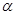 的终边在第一象限,函数
的终边在第一象限,函数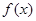 的定义域为
的定义域为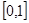 ,且
,且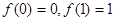 ,当
,当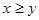 时,有
时,有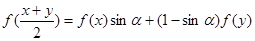 ,则使等式
,则使等式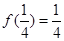 成立的
成立的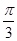 ”是“cos θ≠
”是“cos θ≠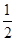 ”的( )
”的( )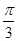 且△ABC的面积等于
且△ABC的面积等于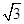 ,求cos(A+B)和a,b的值;
,求cos(A+B)和a,b的值;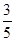 ,sin B=
,sin B=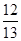 ,求sin C的值.
,求sin C的值.
 .
.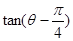 的值;
的值;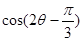 的值.
的值.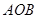 的周长是
的周长是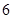 ,圆心角是
,圆心角是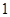 弧度,则该扇形的面积为________.
弧度,则该扇形的面积为________.