题目内容
函数f(x)=
sin(
-x)+4sin
cos
.
(Ⅰ)在△ABC中,cosA=-
,求f(A)的值;
(Ⅱ)求函数f(x)的最小正周期及函数的单调递增区间.
| 2 |
| π |
| 4 |
| x |
| 2 |
| x |
| 2 |
(Ⅰ)在△ABC中,cosA=-
| 3 |
| 5 |
(Ⅱ)求函数f(x)的最小正周期及函数的单调递增区间.
(Ⅰ)∵f(x)=
(
cosx-
sinx)+2sinx=cosx+sinx,
∵在△ABC中,cosA=-
,
∴sinA=
=
,
∴f(A)=cosA+sinA=
;
(Ⅱ)∵f(x)=
(
cosx+
sinx)
=
sin(x+
),
∴函数f(x)的最小正周期T=2π;
由-
+2kπ≤x+
≤
+2kπ(k∈Z)得:-
+2kπ≤x≤
+2kπ(k∈Z),
∴函数f(x)的单调递增区间为[-
+2kπ,
+2kπ](k∈Z).
| 2 |
| ||
| 2 |
| ||
| 2 |
∵在△ABC中,cosA=-
| 3 |
| 5 |
∴sinA=
| 1-cos2A |
| 4 |
| 5 |
∴f(A)=cosA+sinA=
| 1 |
| 5 |
(Ⅱ)∵f(x)=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
∴函数f(x)的最小正周期T=2π;
由-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
∴函数f(x)的单调递增区间为[-
| 3π |
| 4 |
| π |
| 4 |

练习册系列答案
相关题目
 ,使
,使 ; ②函数
; ②函数 是偶函数;
是偶函数;  是函数
是函数 的一条对称轴的方程;
的一条对称轴的方程; 是第一象限的角,且
是第一象限的角,且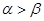 ,则
,则 .
.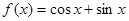 ,
,
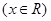 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;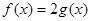 ,求
,求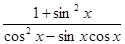 的值.
的值.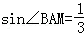 ,则sin∠BAC= _________ .
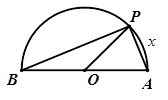
,则sin∠BAC= _________ .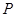 在半径为
在半径为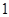 的半圆上运动,
的半圆上运动,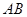 是直径,当
是直径,当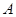 到
到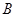 运动时,点
运动时,点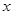 与
与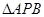 的面积
的面积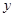 的函数
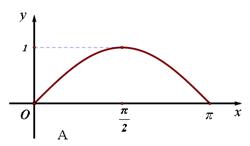
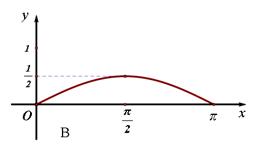
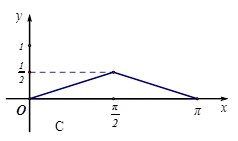
的函数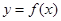 的图像是下图中的( )
的图像是下图中的( )