题目内容
在△ABC中，角A，B，C所对边的边长分别是a，b，c.
(1)若c＝2，C＝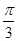
且△ABC的面积等于
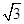，求cos(A＋B)和a，b的值；
(2)若B是钝角，且cos A＝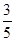
，sin B＝
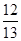，求sin C的值．
(1)若c＝2，C＝
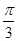且△ABC的面积等于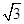，求cos(A＋B)和a，b的值；(2)若B是钝角，且cos A＝
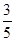，sin B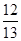＝，求sin C的值．（1）a＝2，b＝2 （2）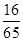
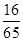
(1)∵A＋B＋C＝π，C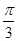＝，∴A＋B＝π－C，
∴cos(A＋B)＝cos(π－C)＝－cos C＝－cos＝－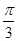
.
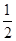由余弦定理及已知条件得a2＋b2－ab＝4，
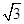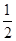又因为△ABC的面积等于，所以absin C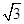＝，得ab＝4.
联立方程组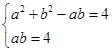
解得a＝2，b＝2.
(2)∵B是钝角，且cos A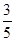＝，sin B＝，
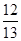∴sin A＝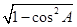
＝ 
＝
，
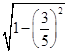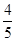cos B＝－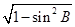
＝－ 
＝－
，
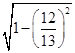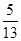∴sin C＝sin[π－(A＋B)]＝sin(A＋B)
＝sin Acos B＋cos Asin B＝×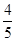
＋×＝.
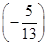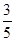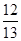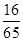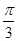，∴A＋B＝π－C，∴cos(A＋B)＝cos(π－C)＝－cos C＝－cos
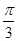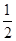＝－.由余弦定理及已知条件得a2＋b2－ab＝4，
又因为△ABC的面积等于
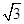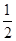，所以absin C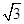＝，得ab＝4.联立方程组
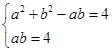
解得a＝2，b＝2.
(2)∵B是钝角，且cos A＝
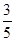，sin B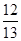＝，∴sin A＝
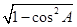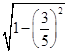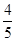＝ ＝，cos B＝－
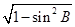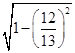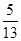＝－ ＝－，∴sin C＝sin[π－(A＋B)]＝sin(A＋B)
＝sin Acos B＋cos Asin B＝
×＋×＝.
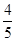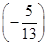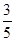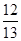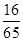练习册系列答案
天天练口算系列答案
相关题目
，
，函数
，
.
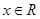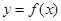的图像的对称中心坐标；
个单位，再向左平移
个单位得函数
的图像，试写出
上的图像.
sinxcosx－2cos2x+l．
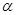∈（0，
），且f（
,使
； ②函数
是偶函数； 
是函数
的一条对称轴的方程；
是第一象限的角，且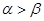
，则
.
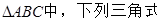①sin(A+B)+sinC;②cos(B+C)+cosA;③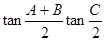
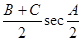,其中恒为定值的是 ( )
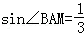，则sin∠BAC= _________ ．
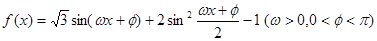为奇函数，且相邻两对称轴间的距离为
．
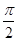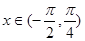时，求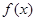
的单调递减区间； 
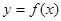的图象沿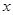
轴方向向右平移
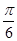个单位长度，再把横坐标缩短到原来的
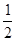（纵坐标不变），得到函数
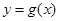的图象．当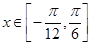
时，求函数
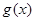的值域．
